Реферат: Типы регулярных регуляторов
p 01 = [( F ( k 1 p 1 + k 2 p 2 ) + k 2 р В.Н )] / F ( k 1 + k 2 ) (12)
Поступление жидкости за бесконечно малый отрезок времени в левую полость исполнительного механизма при расходе Q 1 составляет Q 1 dt . За счёт этого поршень перемещается на величину ds ВЫХ.
Так как объём поступившей жидкости равен приращению объёма левой полости исполнительного механизма, то Q 1 dt = F ds ВЫХ или ds ВЫХ / dt = Q 1 / F 1 .
Подставив в это выражение из (11) значение Q 1 , с учётом (12) получим
ds ВЫХ / dt = [ k 1 k 2 F ( p 1 - p 2 ) - k 1 k 2 f В.Н ] / F 2 ( k 1 + k 2 ) (13)
В этом случае, если можно пренебречь величиной внешней нагрузки р в.н. Уравнение примет вид ds ВЫХ / dt = k D P ВХ , где k = [ k 1 k 2 / ( k 1 + k 2 )] / F ; D P ВХ =p 1 - p 2 ; k – коэффициент передачи интегрирующего звена, значение которого можно изменять в широких пределах с помощью вентилей В1 и В2 .
Таким образом дифференциальное уравнение гидравлического исполнительного механизма имеет вид dx ВЫХ / dt = k x ВХ ; следовательно, в динамическом отношении он является динамическим звеном.
Дифференцирующее звено.
Выходная величина дифференцирующего звена пропорциональна производной по времени от входной величины:
x ВЫХ = k d хВХ / dt (14)
Передаточная функция
W (p) = kp. (15)
Из выражения хВЫХ = k d хВХ / dt следует, что выходная величина дифференцирующее звена пропорциональна скорости изменения входной величины, Если входная и выходная величина имеют одинаковую размерность, то коэффициент k выражается в секундах. В этом случае его принято обозначать Т и называть постоянной времени дифференцирующего звена.
Частотные характеристики идеального дифференцирующего звена с придаточной функцией W (p) = k p имеют вид
W (i w) = j w k; U (w) = 0;
V (w) = w k; W (w) = k w; j (w) = p / 2 (16)
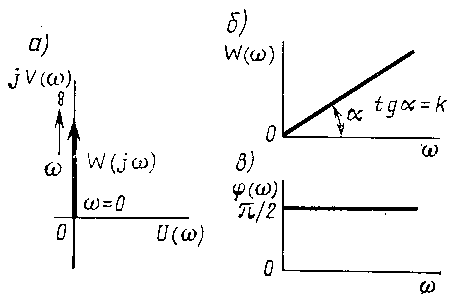
Рисунок 9. Частотная характерика дифференцирующего звена.
В комплексной показательной форме W ( i w ) = w k e j p / 2 . Эти характеристики представлены на рис. 9. Комплексная частотная характеристика дифференцирующего звена совпадает с положительной мнимой полуосью (рис.9а). При всех частотах выходные колебания опережают по фазе входные колебания на угол 90°, т.к. фазочастотная характеристика не зависит от частоты и равна p / 2 (рис.9в).
Амплитудно-частотная характеристика W ( w ) имеет вид прямой линии, проходящей через начало координат под углом a = arctg k .
Чем больше частота входных колебаний, тем больше они усиливаются звеном. При малых частотах (w = 0 ) сигнал через звено не проходит (рис.9б). Скачкообразное единичное изменение входной величины вызывает мгновенное изменение выходной величины от 0 до ¥ и мгновенный спад её от ¥ до 0.
Логарифмируя W ( w ) в выражении (16), получаем
L (w) = 20 lg k + 20 lg w (17)
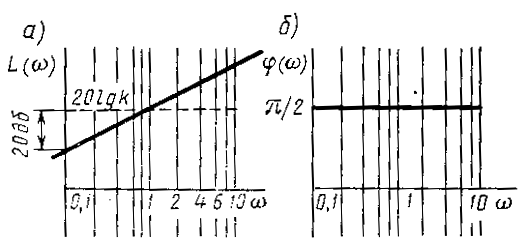
Рисунок 10. Логарифмические частотные характеристики частотного звена.
Логарифмическая амплитудно-частотная характеристика (ЛАЧХ) дифференцирующего звена представляет собой прямую (рис. 10а) с наклоном +20 дБ / дек, ордината, которой при w = 1 равна 20 lg k .
Фазочастотная характеристика звена в полулогарифмическом масштабе в соответствии с (16) представлена на рис.10б.
Примером дифференцирующего звена может служить тахогенератор, если за его входную величину принять угол поворота его вала bВХ , а за выходную величину – напряжение U ВЫХ тахогенератора, т.к. последнее пропорционально угловой скорости wВЫХ , которая, в свою очередь, равна производной от угла поворота U ВЫХ = kВХ = k d b ВХ / dt .
Реальное интегрирующее звено.
В динамическом отношении реальное интегрирующее звено определяется дифференциальным уравнением
T d 2 x ВЫХ / dt 2 + dx ВЫХ / dt = k x ВХ (18)
Передаточная функция звена