Реферат: Типы регулярных регуляторов

Из этого выражения следует, что реальное интегрирующее звено можно рассматривать как последовательное соединение идеального интегрирующего и апериодического звеньев. Коэффициент k реального интегрирующего звена равен коэффициенту передачи идеального интегрирующего звена.

Постоянная времени Т определяет инерционность процесса интегрирования. При этом чем меньше Т, тем больше по своим свойствам реальное интегрирующее звено приближается к идеальному интегрирующему. Примером реального интегрирующего звена может служить электро двигатель, если в динамическом отношении нельзя пренебречь его электромеханической инерцией. В этом случае связь между напряжением двигателя u _ВЫХ и его углом поворота b _ВЫХ определяется дифференциальным уравнением

T_M d ² b _ВЫХ / dt ² + d b _ВЫХ / dt = k u _ВХ (20)

где Т _M – постоянная времени, определяемая инерционностью якоря двигателя и перемещаемых этим двигателем масс; k – коэффициент передачи двигателя по каналу: подводимое напряжение к двигателю – угловая скорость двигателя.

Из выражения (20) следует, что в рассматриваем случае в динамическом отношении электродвигатель является реальным интегрирующим звеном и его передаточная функция определяется выражением (19).

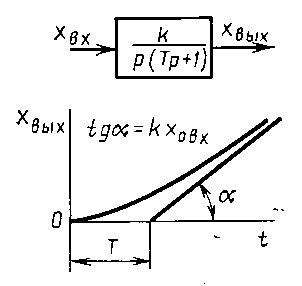
Рисунок 11. Передаточная функция и переходной процесс реального интегрирующего звена.

На рис.11 представлен характер изменения выходной величины x _ВЫХ реального интегрирующего звена при подаче на вход постоянного сигнала x _0ВХ

Реальное дифференцирующее звено.

Дифференциальное уравнение реальное дифференцирующего звена имеет вид

T dx _ВЫХ / dt + x _ВЫХ = k dx _ВХ / dt (21)

С учётом этого передаточная функция звена

W (p) = k p / (T p + 1) (22)

Таким образом, реальное дифференцирующее звено можно рассматривать как последовательное соединение идеального дифференцирующего звена и апериодического звена. При этом, чем меньше постоянная времени Т , тем больше реальное дифференцирующее звено приближается к идеальному дифференцирующему.

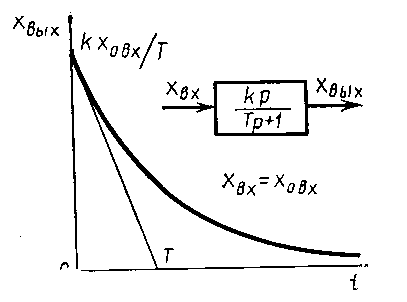
Рисунок 12. Передаточная функция и переходной процесс реального дифференцирующего звена.

Переходный процесс реального дифференцирующего звена представлен на рис.12. Чем меньше Т , тем ближе реальное дифференцирующее звено приближается к идеальному. Если Т стремится к нулю, то получаем идеальное дифференцирующее звено с коэффициентом передачи k .

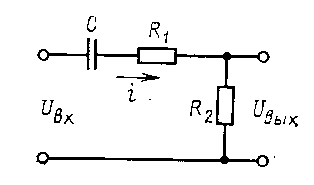
Рисунок 13. Схема реального дифференцирующего звена.

Пример. Определим динамическиесвойства RC-цепи, представленной на рис.13, для которой

u _ВЫХ = (1 / C) ¦ i dt + i R₁ + u _ВЫХ ; u _ВЫХ = i R₂ . (23)

Преобразуя эти уравнения по Лапласу, получаем

R ₂ C p U _ВХ ( p ) = [1 + C ( R ₁ + R ₂ ) p ] U _ВЫХ ( p ) (24)

Передаточная функция цепи

W (p) = k Т p / (T p + 1) (25)

Таким образом, в динамическом отношении RC-цепь (рис.13) является реальным дифференцирующим звеном.

Постоянная времени и коэффициент передачи звенаk = R ₂ / ( R ₁ + R ₂ ); T = C ( R ₁ + R ₂ ) .

Изображение выходной величины при скачкообразном изменении входной величины до х_0ВХ

Типы регулярных регуляторов (PID) ПИД.

УУ	ОР

Сигнал

ОС

Сумматор Упр. Устройство Обр. Связь Орг. Регистр.

Тепловые регуляторы.

Регулятор с пропорциональным законом регулирования называется пропорциональным регулятором или П-регулятором.

В динамическом отношении П-регуляторы являются усилительным звеном.