Использование z -преобразования позволяет преобразовать трансцендентный полином в степенной, что позволяет упростить процесс исследования дискретных систем управления.

Применение z -преобразования (рис. 2.3) отображает основную полосу на плоскость Z , отрезок мнимой оси в окружность единичного радиуса, а левую часть полосы в круг единичного радиуса.

Следовательно, дискретная система устойчива, если все корни ее характеристического уравнения расположены в левой полуплоскости в пределах основной полосы (т. е. условие устойчивости ).

Пример 3. Определить устойчивость дискретной системы с передаточной функцией

.

Характеристическое уравнение имеет вид

.

Определим корни характеристического уравнения

Определим модуль корней

.

Система не устойчива, так как модуль корней ее характеристического уравнения меньше единицы.

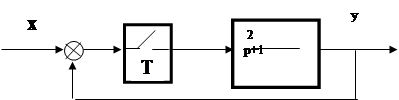
Пример 4. Определить устойчивость дискретной системы, структурная схема которой представлена на рис. 2.

-

Рис. 2

Решение: Передаточная функция разомкнутой дискретной системы

.

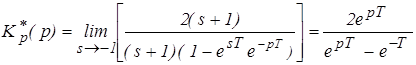Передаточная функция разомкнутой дискретной системы в форме z - преобразования

, где .

Передаточная функция замкнутой дискретной системы в форме z - преобразования

.

Характеристическое уравнение имеет вид .

Определим корни характеристического уравнения

При этом модуль корня при любых допустимых T , следовательно, система устойчива.

3. Определение устойчивости дискретных систем в форме w - преобразования

Из теории функций комплексного переменного известно, что билинейное преобразование (w -преобразование, преобразование Мизеса) отображает круг единичного радиуса в плоскости Z во всю левую полуплоскость плоскости W , при использовании подстановки

или. (4)

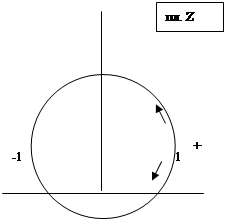
Установим связь между плоскостями Z и W (см. рис. 3).

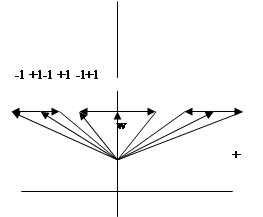Рис. 3

1. При½z ½ = 1 ,½w+1 ½ = ½w-1 ½, что соответствует оси j.

2. При½z ½ < 1 ,½w+1 ½ < ½w-1 ½ - соответствует левой полуплоскости пл. W .

3. При½z ½ > 1 ,½w+1 ½ > ½w-1 ½ - соответствует правой полуплоскости.