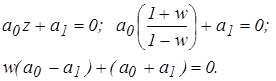
Условие устойчивости: a₀ > 0, a₁ > 0, а также: a₀ - a₁ > 0.

При n = 2 характеристическое уравнение имеет вид

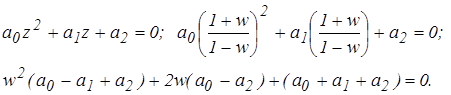
Условие устойчивости: a₀ > 0, a₁ > 0, a₂ > 0, а также:

a₀ - a₁ + a₂ > 0, a₀ - a₂ > 0.

Пример Определить устойчивость дискретной системы, если передаточная функция разомкнутой системы в форме z – преобразования, имеет вид

.

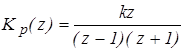Передаточная функция замкнутой дискретной системы в форме z – преобразования

.

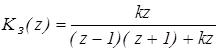Характеристическое уравнение имеет вид

.

Выполним билинейное преобразование

Система не устойчива.

Критерий устойчивости Михайлова

Доказательство частотных критериев устойчивости базируется на следствии из принципа аргумента. Рассмотрим, как он формулируется для дискретных систем.

Пусть задано характеристическое уравнение замкнутой системы

. (8)

Рассмотрим комплексную плоскость Z (рис. 7), пусть z₂ расположен внутри круга единичного радиуса, а z₁ вне него.

При этом

(9)

Если замкнутая система устойчива, то все корни расположены в пределах окружности единичного радиуса, а значит

(10)

Замкнутая дискретная система устойчива, если характеристическая кривая D*(jw) при изменении частоты 0 £w£p/T последовательно проходит 2n квадрантов.

Порядок построения характеристической кривой: определяем D(z) ; выполняем подстановку ; определяем выражение

;

изменяя 0 £ w £ p /T строим D*(j w ) (рис. 5).

а) б)

Рис. 5