Следовательно, при использовании билинейного преобразования условия устойчивости непрерывных систем можно использовать для дискретных систем управления.

Пример 5. Определить устойчивость дискретной системы с передаточной функцией

.

Характеристическое уравнение имеет вид

.

Определим корни характеристического уравнения

Система устойчива, так как корни ее характеристического уравнения расположены в левой полуплоскости.

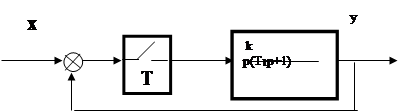
Пример 6. Определить устойчивость дискретной системы, структурная схема которой представлена на рис. 4.

-

Рис. 4

Решение: Передаточная функция разомкнутой дискретной системы в форме z – преобразования

, где .

Передаточная функция замкнутой дискретной системы

.

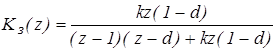Характеристическое уравнение системы имеет вид

.

Выполнив билинейное преобразование, получим

Условие устойчивости: 1 – b > 0, 1 + b +d > 0, где b = [k(1-d)-(1+d)].

4. Применение критериев устойчивости для дискретных систем

Все критерии устойчивости, которые используются для анализа устойчивости непрерывных систем, могут быть использованы для дискретных систем с учетом некоторых особенностей.

Критерий Гурвица

Критерий устойчивости Гурвица можно использовать при применении билинейного преобразования. Рассмотри алгоритм его использования.

1. Записываем характеристическое уравнение D(z) = 0

.(5)

2. Выполняем подстановку , при этом получим характеристическое уравнение D(w) = 0 , т. е. в форме билинейного преобразования

. (6)

3. Составляем определитель Гурвица

. (7)

4. Определяем устойчивость также как и для непрерывных систем.

Линейная дискретная система устойчива, если при определитель Гурвица и все его диагональные миноры положительны.

Рассмотрим частные случаи.