Шпаргалка: Лекции по матану (III семестр) переходящие в шпоры

2)Пусть = ¥ тогда из(5) следует, что для любого х ÎR Итак ряд (1) сходится при любом х причем абсолютно.

3) Пусть =0 тогда из (5) следует, что и ряд расходится для любого х. Он сходится только при х = 0 В этом сл-е R = 0.

Т3 Если существует предел конечный или бесконечный , то (10)

№15

1 условия

существования и вычисления

криволинейных интегралов.

Кривая L наз. гладкой, если ф-ции j(t), y(t) из определяющих её параметрических уравнений:

(1)

имеет на отрезке [a,b] непрерывные производные: j’(t), y’(t).Точки кривой L наз особыми точками, если они соответствуют значению параметра tÎ [a,b] для которых (j’(t))² +(y’(t))² = 0 т. е. обе производные обращаются в 0. Те точки для которых сие условие не выполняется наз. обычными (ВАУ!).

Если кривая L=AB задана ф-лами (1), является гладкой и нет имеет обычных точек, а ф-ции f(x,y), P(x,y), Q(x,y) непрерывны вдоль этой кривой, то криволинейные интегралы всех видов существуют (можно даже ихние формулы нарисовать для наглядности) и могут быть вычислены по следующим формулам сводящим эти интегралы к обычным:

Отседова жа вытекаает штаа:

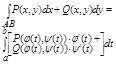
В частности, если кривая АВ задана уравнением y = y(x), a<=x<=b , где у(х) непрерывно дифференцируемая ф-ция, то принимая х за параметр t получим:

ну и сумма там тожжа упростица.

ну и наоборот тожжа так будит, если х = х(у)

Если АВ задана в криволинейных координатах a <= j <= b где ф-ция r(j) непрерывно дифференцируема на отрезке [a, b] то имеет место частный случай, где в качестве параметра выступает полярный угол j. x = r(j)×cos(j),

y= r(j)×sin(j).

и у второго рода так же.

Прямая L наз кусочно-гладкой, если она непрерывна и распадается на конечное число не имеющих общих внутренних точек кусков, каждый из которых представляет собой гладкую кривую. В этом случает криволинейные интегралы по этой кривое определяются как сумма криволинейных интегралов по гладким кривым составляющим сию кусочно-гладкую кривую. все выше сказанное справедливо и для пространственной кривой (с буквой зю).

2 Свойства степенных рядов

Т1 Если степенной ряд (1) имеет радиус сходимости R>0, то на любом отрезке действительной оси вида |x|<=r, 0<r<R (2) (или [-r,r]) целиком лежащем внутри интервала сходимости ряд (1) сходится равномерно.

Для ряда отрезком равномерной сходимости будет отрезок |x-x0|<=r или ([x0-r,x0+r])

Т2 На любом отрезке |x-x0|<=r сумма степенного ряда является непрерывной ф-цией.

Т3 Радиусы сходимости R, R1, R2 соответственно рядов×(5), (6), (7) равны: R1=R2=R3. Итак ряды (6) и (7) полученные с помощью формального интегрирования и дифференцирования имеют те же радиусы сходимости, что и исходный ряд.

Пусть ф-ция f(x) является суммой степенного ряда (9)

Т4 Дифференцирование степенного ряда