Шпаргалка: Лекции по матану (III семестр) переходящие в шпоры

Отрезок [a,b] – проекция Д на ось ох. Для такой области людбая прямая, параллельная оу и проходящая через внутреннюю точку области Д пересекает границу области не более чем в 2 точках. Такая область наз. правильной в направлении оси оу.

Если фция f(x,y) задана на Д и при каждом х Î [a,b] непрерывна на у , на отрезке, [y1(x),y2(x)], то фц-ия F(x) = , наз. интегралом, зависящим от параметра I, а интеграл : , наз повторным интегралом от ф-ции f(x,y) на области Д. Итак, повторный интеграл вычисляется путем последовательного вычисления обычных определенных интегралов сначала по одной., а затем по другой переменной.

2 Необходимый

признак сходимости рядов

Если ряд сходится, то предел его общего члена равен нулю:

Док-во:

Sn=u1+u2+…+un

Sn-1\u1+u2+…+un-1

un=Sn-Sn-1, поэтому:

Сей признак является только необходимым, но не является достаточным., т. е. если предел общегоь члена и равен нулю совершенно необязательно чтобы ряд при этом сходился. Следовательно, вот сие условие при его невыполнении является зато достаточным условием расходимости ряда.

№5

1 Замена переменных в двойном интеграле.

Общий случай криволинейных координат

Пусть существует ф-ция f(x,y) интегр на области Д, можно прямолинейные координаты x, y с помощью формул преобразования перейти к криволинейным: x = x(u,v), y=y(u,v), где эти ф-ции непрерывные вместе с частными производными первого порядка, устанавливают взаимно однозначное и в обе стороны непрерывное соответствие между точками плоской области Д и области Д’ и определитель преобразования, наз. Якобианом не обращается в 0: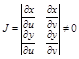если это выполняется можно пользоваться ф-лой:

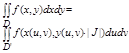
2 Интегральный признак

сходимости ряда. Ряд Дирихле

Т1 Пущай дан рядт (1), члены которого неотрицательны, и не возрастают: u1>=u2>=u3…>=un

Если существует ф-ция f(x) неотрицательная, непрерывная и не возрастающая на [1,+¥] такая, что f(n) = Un, "nÎN, то для сходимости ряда (1) необходимо унд достаточно, чтобы сходился несобственный интеграл:, а для расходимости достаточно и необходимо чтобы сей интеграл наоборот расходился (ВАУ!).

Применим сей признак для исследования ряда Дирихле: Вот он: , aÎR Сей ряд называют обобщенным гармоническим рядом, при a >0 общий член оного un=1/n^a -0 и убывает поэтому можно воспользоваться интегральным признаком, функцией здеся будет ф-ция f(x)=1/x^a (x>=1)сия ф-ция удовлетворяет условиям теоремы 1 поэтому сходимость (расходимости) ряда Дирихле равнозначна сходимости расходимости интеграла:

Возможны три случая:

1 a>1,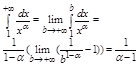

Интеграл а потому и ряд сходится.

2 0<a<1,

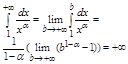
Интеграл и ряд расходится

3 a=1,

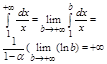
Интеграл и ряд расходится

№ 6

1 Двойной интеграл

в полярных координатах

Переход к полярным координатам частный случай замены переменных.

Луч, проходящий из произв точки О имеет на плоскости полярные координаты A(r, j) где r = |ОA | расстояние от О до А полярный радиус. j = угол между векторами ОА и ОР – полярный угол отсчитываемой от полярной оси против часовой стрелки. всегда 0<=r<=+¥, 0<=j <=2p .