Шпаргалка: Лекции по матану (III семестр) переходящие в шпоры

1 Определение криволинейных

интегралов 1 и 2 рода

Криволинейный интеграл по длине дуги (1 рода)

Пусть ф-ция f(x,y) определена и непрерывна в точках дуги АВ гладкой кривой К. Произвольно разобъем дугу на n элементарных дуг точками t0..tn пусть Dlk длина k частной дуги. Возьмем на каждой элементарной дуге произвольную точку N(xk,hk) и умножив сию точку на соотв. длину дуги составим три интегральную суммы:

d1 = f(xk,hk)×Dlk

d2 =Р(xk,hk)×Dхk

d3 = Q(xk,hk)×Dyk,

гдеDхk = x_k -x_k-1 , Dyk = y_k -y_k-1

Криволинейным интегралом 1 рода по длине дуги будет называться предел интегральной суммы d1 при условии, что max(Dlk) - 0

Если предел интегральной суммы d2 или d3 при l- 0, то этот предел наз. криволинейным интегралом 2 рода, функции P(x,y) или Q(x,y) по кривой l = AB и обозначается:

или

сумму: + принято называть общим криволинейным интегралом 2 рода и обозначать символом:

в этом случае ф-ции f(x,y), P(x,y), Q(x,y) – называются интегрируемыми вдоль кривой l = AB. Сама кривая l наз контуром или путем интегрирования А – начальной, В – конечной точками интегрирования, dl – дифференциал длины дуги, поэтому криволинейный интеграл 1 рода наз. криволинейным интегралом по дуге кривой, а второго рода – по функции..

Из определения криволинейных интегралов следует, что интегралы 1 рода не зависят от того в каком направлении от А и В или от В и А пробегается кривая l. Криволинейный интеграл 1 рода по АВ:

, для криволинейных интегралов 2 рода изменение направления пробегания кривой ведет к изменению знака:

В случае, когда l – замкнутая кривая т. е. т. В совпадает с т. А, то из двух возможных направлений обхода замкнутого контура l называют положительным то направление, при котором область лежащая внутри контура остается слева по отношению к ??? совершающей обход, т. е. направление движения против часовой стрелки. Противоположное направление обхода наз – отрицательным. Криволинейный интеграл АВ по замкнутому контуру l пробегаемому в положит направлении будем обозначать символом:

Для пространственной кривой аналогично вводятся 1 интеграл 1 рода:

и три интеграла 2 рода:

сумму трех последних интегралов наз. общим криволинейным интегралом 2 рода.

2 Радиус сходимости и интервал сходимости степенного ряда.

Рассмотрим степенной ряд:

(1) Число (конечное или бесконечное) R>=0 наз радиусом сходимости ряда (1) если для любого х такого, что |x|<R ряд (1) сходится, а для " х таких. что |x|>R ряд расходится Интервал на числовой оси состоящий из т. х для которых |x|<R, т. е. (-R, +R) наз. интервалом сходимости.

Т1 Для всякого степенного ряда (1) существует радиус сходимости R 0<=R<=+¥ при этом, если |x|<R, то в этой т. х ряд сходится абсолютно

Если вместо х взять у = х-х0, то получится: интервал сходимости: |x-x0<R| будет: (x0-R, x0+R)При этом если |x-x0|<R? то ряд сходится в т. x абсолютно иначе расходится. На концах интервала, т. е. при x = -R, x=+R для ряда (1) или x = x0-R, x=x0+R для ряда (3) вопрос о сходимости решается индивидуально. У некоторых рядов интервал сходимости может охватывать всю числовую прямую при R = +¥ или вырождаться в одну точку при R = 0.

Т2 Если для степенного ряда (1) существует предел (конечный или бесконечный): , то радиус сходимости будет равен этому пределу.

Док-вы: Рассмотрим ряд из абсолютных величин и по Даламберу исследуем его на сходимость:

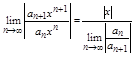(5)