Шпаргалка: Лекции по матану (III семестр) переходящие в шпоры
1. Двойной интеграл по области D = площади этой области.
2. Если область G содержится в Д, а ф-ция ограничена и интегрируема в Д, то она интегрируема и в G.
3. Аддитивное св-во. Если область Д при помощи кривой г разбивают на 2 области Д1 и Д2, не имеющих общих внутренних точек, то: 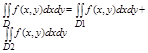
4. константы выносятся за знак интеграла, а сумму в ф-ции можно представить в виде суммы интегралов:
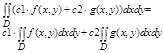
5. Если ф-ции f и g интегрируемы в Д, то их произведение также интегрируемо в Д. Если g(x,y) ¹ 0 то и f/g интегрируема в Д.
6. Если f(x,y) и g(x,y) интегрируемы в Д и всюду в этой области f(x,y) <= g(x,y), то:
![]()
В частности: g(x,y) >=0 то и
![]()
7. Оценка абсолютной величины интеграла: если f(x,y) интегрируема в Д, то и |f(x,y)| интегрир. в Д причем
![]()
обратное утверждение неверно, итз интегрируемости |f| не следует интегрируемость f.
8. Теорема о среднем значении.
Если ф-ция f(x,y) интегр. в Д., то в этой области найдется такая точка (x, h) Î Д, что:
![]() (2), где S – площадь фигуры Д. Значение f(x, h) опред по ф-ле (2) наз. средним значением ф-ции f по области Д.
(2), где S – площадь фигуры Д. Значение f(x, h) опред по ф-ле (2) наз. средним значением ф-ции f по области Д.
2 С-ва сходящихся рядов
Пусть даны два ряда: u1+u2+…un =![]() (1) и v1+v2+…vn =
(1) и v1+v2+…vn = ![]() (2)
(2)
Произведением ряда (1) на число lÎR наз ряд: lu1+lu2+…lun =![]() (3)
(3)
Суммой рядов (1) и (2) наз ряд:
(u1+v1)+(u2+v2)+…(un+vn) = ![]() (для разности там только - появица)
(для разности там только - появица)
Т1 Об общем множителе
Если ряд (1) сходится и его сумма = S, то для любого числа l ряд ![]() =l×
=l×![]() тоже сходится и его сумма S’ = S×l Если ряд (1) расходится и l¹ 0, то и ряд
тоже сходится и его сумма S’ = S×l Если ряд (1) расходится и l¹ 0, то и ряд ![]() тоже расходится. Т. е. общий множитель не влияет на расходимости ряда.
тоже расходится. Т. е. общий множитель не влияет на расходимости ряда.
Т2 Если ряды (1) и (2) сходятся, а их суммы = соотв S и S’, то и ряд: ![]() тоже сходится и если s его сумма, то s = S+S’. Т. е. сходящиеся ряды можно почленно складывать и вычитать. Если ряд (1) сходится, а ряд (2) расходится, то их сумма(или разность) тоже расходится. А вот если оба ряда расходятся. то ихняя сумма (или разность)может как расходится (если un=vn) так и сходиться (если un=¹vn)
тоже сходится и если s его сумма, то s = S+S’. Т. е. сходящиеся ряды можно почленно складывать и вычитать. Если ряд (1) сходится, а ряд (2) расходится, то их сумма(или разность) тоже расходится. А вот если оба ряда расходятся. то ихняя сумма (или разность)может как расходится (если un=vn) так и сходиться (если un=¹vn)
Для ряда (1) ряд ![]() называется n – ным остатком ряда. Если нный остаток ряда сходится, то его сумму будем обозначать: rn =
называется n – ным остатком ряда. Если нный остаток ряда сходится, то его сумму будем обозначать: rn = ![]()
Т3 Если ряд сходится, то и любой его остаток сходится, если какой либо остаток ряда сходится, то сходится и сам ряд. Причем полная сумма = частичная сумма ряда Sn + rn
Изменение, а также отбрасывание или добавление конечного числа членов не влияет на сходимость (расходимость) ряда.
№4
1 Сведение
2ного интеграла к повторному
Пусть у1(х), у2(х) непрерывны на отрезке [a, b], у1(х)<= у2(х) на всем отрезке.