Шпаргалка: Лекции по матану (III семестр) переходящие в шпоры

Якобиан преобразования будет равен:

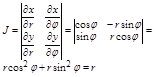И формула при переходе примет вид:

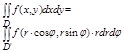
2 Признаки сравнения

Т(Признаки сравнения)

Пущай и ряды с неотрицательными членами и для любого n выполняется нер-во:

un<=vn (1)тогда

1 Если ряд vn сходится, то сходится и ряд un

2 если ряд un расходится, то расходится и ряд vn. Т. е. говоря простыми русскими словами для простых русских людей (ну для дураков вроде тебя): Из сходимости ряда с большими членами следует сходимость ряда с меньшими, а из расходимости ряда с меньшими членами следует расходимости ряда с большими и не наоборот!!!

Причем можно требовать, чтобы неравенство (1) выполнялось не для всех номеров n, а начиная с некоторого n0, т. е. для некоторых номеров меньших n0 неравенство (1) может и не выполняться. При применении сего признака сравнения удобно в качестве ряда сравнения брать ряд Дирихле или геометрический ряд, с которыми и так уже все ясно.

Т3 Засекреченная

Если сущ вышеописанные неотр. ряды, то если сущ предел:

(0<k<+¥) тада оба эти ряда сходятся.

№7

1 Вычисление

площади плоской области

с помощью 2ного интеграла

Если Д правильная в направлении оу a<=x<=b, y1(x)<=y<=y2(x), то

Если Д огр линиями в полярных координатах, то

2 Признаки Даламбера и Коши

Т(Признак Далембера)

Пущай для ряда un с положит членами существует предел:

, то

1 Если k<1, то ряд сходится

2 Если k>1 ряд расходится

Т(Признак Коши)

Пусть для того же самого ряда (т. е. положительного) существует предел:, тогда

1 Если k<1, то ряд сходится