Статья: Исторические проблемы физики. Сила, масса, инерциальная система отсчета

Выбор ИСО, не связанной ни с одним из взаимодействующих тел, движущейся ускоренно относительно каждого из тел и притом с разными ускорениями объясняется именно тем, что при этом достигается однозначность характеристик каждого из взаимодействующих тел.

Коэффициенты

Исходные формулы при построении систем единиц динамики Ньютона следующие: ,

.

В системе единиц, предложенной В. Томпсоном, оба коэффициента принимаются равными единице:

,

при этом сам эталон массы оказывается вполне определенным (~ 15 т, при единице длины - см и единице времени - с).

Покажем, как появляются коэффициенты в формулах Ньютона в случае, если эталон массы выбирается произвольно.

Пусть, например, новый эталон массы составляет томсоновых эталонов (g имеет произвольное, отличное от единицы числовое значение).

Тогда: .

В системе единиц типа “динамической” :

.

Поскольку: , и , ,

то получаем: или , откуда .

В системе единиц типа “гравитационной” :

.

Второй закон Ньютона: в новой системе единиц:

или откуда: .

В частном случае, когда коэффициент  в точности равен “гравитационной постоянной”, мы получаем собственно гравитационную и собственно динамическую системы единиц.

Если новый эталон массы, измеряемый в долях от томсонова эталона массы, сохраняет прежнюю размерность [см3/c2] , то коэффициент  есть число, показывающее во сколько раз новый эталон больше или меньше томсонова эталона.

Если же новому эталону дано и новое название (например, грамм), то коэффициент  приобретает размерность:

.

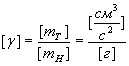Итак, гравитационная и динамическая постоянные появляются вследствие произвольности выбора эталона массы при построении систем единиц измерения и не имеют собственного физического смысла.

Случай больших скоростей

Если считать установленным существование предельной относительной скорости перемещения взаимодействующих тел, при приближении к которой их ускорения стремятся к нулю по формулам:

, ( при ),

где - ускорение при относительных скоростях , много меньших скорости света , то и сила взаимодействия

, ( при ).

Вообще говоря, может означать либо по формуле , либо по формуле 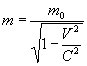, поскольку .