Статья: Исторические проблемы физики. Сила, масса, инерциальная система отсчета

Он устанавливает фактически способ определения СО1 в качестве местной ИСО относительно некоторых, вполне определенных для данной СО1 и данной точности измерений галилеевских объектов с помощью самих этих объектов.

Его заключение таково: “Данный эксперимент устанавливает, что для данных галилеевских объектов данное небесное тело является телом достаточно большой массы , чтобы его СО1 для данных галилеевских объектов и при данной точности измерений могла быть принята в качестве местной ИСО”.

Для тела 1 с малой массой или тела 2 с большой массой он бы получил другой результат, чтобы констатировать в свою очередь: “Эксперимент устанавливает, что для данных объектов данная СО1 с точностью, определяемой точностью измерений, не может считаться местной ИСО” или иначе: “Данные объекты относительно ИСО = СО1 с точностью, определяемой точностью измерений, не могут считаться галилеевскими объектами, имеющими бесконечно малую массу относительно ”.

Посмотрим теперь, как выглядит эксперимент Галилея в общем случае, вначале для произвольной массы , затем для произвольной массы .

Определим предварительно требуемые условия проведения эксперимента.

Пусть мы желаем наблюдать падение тела 2' большой массы в два раза быстрее падения тела 2" галилеевской массы.

Это значит, что за время прохождения телом 2' пути (где - высота Пизанской башни) тело 2" проходит путь .

Поэтому в СО1, где тело 1 - Земля (объект много большей массы ) тела 2' и 2" имеют разные ускорения , , причем .

Поскольку ускорение любого тела 2 в СО1 равно:

,

то имеем: для галилеевского объекта , .

Для искомого объекта большой массы :

.

Но .

Следовательно , , т.е. .

Таким образом выясняется, что искомый объект 2' большой массы и одинаковой геометрии с галилеевским объектом должен иметь массу , равную массе Земли (очевидно при этом, что бросать объекты 2' и 2" можно только поочередно, а после броска тела 2' убирать его куда-нибудь подальше, скажем, за орбиту Луны).

Поэтому полученное Галилеем равенство ускорений есть всего лишь результат “удачно” выбранных галилеевских объектов.

Оценим порядок величин, которые пытался обнаружить Галилей.

Пусть , .

Опережение телом 2' тела 2" в СО1 составляет:

,

где , , т.е. .

При с,

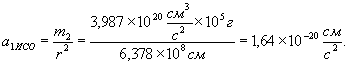
Откуда .

Если теперь выбрать в качестве тела 1 тело пренебрежимо малой массы , то при измерениях в СО1 галилеевский объект массой действительно обладает в 2 раза большим ускорением , в полном соответствии с “опровергаемым” положением Аристотеля.

Для этого достаточно обеспечить при массе дробинки г и ядра кг массу Земли, вместе с находящейся на ней Пизанской башней и экспериментатором-физиком, равную, скажем, г.

При этом, однако, возникает новая трудность: при и имеем: .

При таком ускорении путь м будет пройден за время , равное: