Учебное пособие: Численные методы для решения нелинейных уравнений
Операции сложения элементов и умножения их на числа удовлетворяют законам дистрибутивности:
1. ![]() ,
,
2. ![]() .
.
Каждой паре элементов ![]() поставлено в соответствие действительное число, обозначаемое символом
поставлено в соответствие действительное число, обозначаемое символом ![]() и называемое скалярным произведением, где
и называемое скалярным произведением, где
![]()
и выполнены следующие условия:
1. ![]() ,
,
2. ![]() ,
,
3. ![]() ,
,
4. ![]() , причем
, причем ![]() – нулевой элемент.
– нулевой элемент.
Матрица ![]() вида
вида
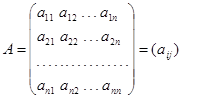
![]() , (1)
, (1)
где ![]() – действительные числа (
– действительные числа (![]() ,
,![]() ) определяет линейный оператор, отображающий линейное пространство
) определяет линейный оператор, отображающий линейное пространство ![]() в себя, а именно, для
в себя, а именно, для ![]()
![]() ,
,
где ![]() .
.
Над линейными операторами, действующими в линейном пространстве ![]() , вводятся следующие операции:
, вводятся следующие операции:
1. сложение операторов ![]() , при этом, если
, при этом, если ![]() , то
, то ![]() ,
,
2. умножение операторов на числа: ![]() при этом, если
при этом, если ![]() , то
, то ![]() ,
,
3. умножение операторов: ![]() , при этом, если
, при этом, если ![]() , то
, то ![]() .
.
Обратным к оператору ![]() называется оператор
называется оператор ![]() такой, что
такой, что ![]() , где
, где ![]() – единичный оператор, реализующий тождественное отображение, а именно,
– единичный оператор, реализующий тождественное отображение, а именно,
 .
.
Пусть число ![]() и элемент
и элемент ![]() , таковы, что
, таковы, что ![]() .
.
Тогда число ![]() называется собственным числом линейного оператора
называется собственным числом линейного оператора ![]() , а элемент
, а элемент ![]() – собственным вектором этого оператора, соответствующим собственному числу
– собственным вектором этого оператора, соответствующим собственному числу ![]() .
.
Линейный оператор ![]() называется сопряженным к оператору
называется сопряженным к оператору ![]() , если для любых элементов
, если для любых элементов ![]() выполняется равенство
выполняется равенство ![]() .
.
Для всякого оператора ![]() сопряженный оператор
сопряженный оператор ![]() существует, единствен; если
существует, единствен; если ![]() , то
, то ![]() .
.
Справедливы равенства:
1. ![]() ,
,
2. ![]() ,
,
3. ![]() ,
,