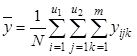Учебное пособие: Дисперсионный анализ при помощи системы MINITAB для WINDOWS
2) Qx2 -по фактору x2 ,
3) Qe -остаточную сумму квадратов, зависящую от ошибки e,
4) Q x1x2 -зависящую от взаимодействия (произведения) x1 x2 двух факторов.
В этом случае по выборочным значениям вычисляются:
1) среднее 
для каждого уровня фактораx1 :
;
2) среднее 
для каждого уровня фактора x2 :
;
3) общее среднее 
по всем N опытам, т.е. по всем m параллельным опытам на всех сочетаниях уровней факторов x1 и x2 (
):
;
4) среднее 
по m параллельным опытам для каждого сочетания уровней факторов x1 и x2 :
.
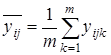В табл.2 показаны данные полного факторного эксперимента с одинаковым числом наблюдений в ячейках.
Таблица 3. - Данные эксперимента и расчёты средних при двухфакторном дисперсионном анализе
|
j = | 1 | 2 | … |  |  | |
 i = | k |  |  | … |  | |
|
1 | 1 |  | ||||
| 2 |  | |||||
| … | … | |||||
| m |  | |||||
|
. . . | 1 | |||||
| 2 | ||||||
| … | ||||||
| m | ||||||
|
| 1 | |||||
| 2 | ||||||
| … | ||||||
| m | ||||||
|
|
| |||||
В табл.2 
вычисляется по выделенной части столбца, содержащей m параллельных опытов.
Общая сумма квадратов отклонений Q0 рассчитывается по формуле:
Эту сумму можно разложить на 4 составляющие:
1) сумму, характеризующую влияние фактора x1 :
;
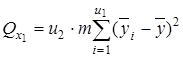2) сумму, характеризующую влияние фактора x2 :