Учебное пособие: Елементи теорії відносності та основне рівняння ідеального газу
![]()
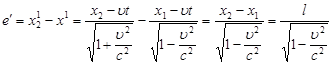 , тобто
, тобто ![]() .
.
Проміжок часу між двома подіями в обох системах буде рівний:
![]()
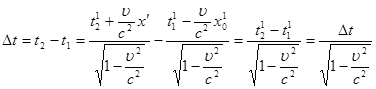 , тобто
, тобто ![]() .
.
В системі координат, відносно якої тіло рухається, тривалість події більша ніж в системі координат, відносно якої тіло рухається, а рухомий годинник іде повільніше, ніж годинник в системі s.
Закон додавання швидкостей:
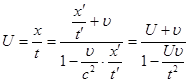 .
.
Таким чином, з перетворень Лоренца випливає, що розміри тіл залежать від швидкості їхнього руху:
![]() (3)
(3)
Протікання процесів в системі, що рухається, затримується:
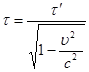 ,
, ![]() (4)
(4)
Закон додавання швидкостей набуває вигляд:
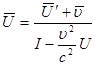 (5)
(5)
Із перетворень Лоренца видно, що просторові координати пов’язані з часом. Отже, простір і час взаємозв’язані і утворюють єдине ціле – час. В теорії відносності простір-час розглядається як абсолютна форма існування матерії.
В теорії відносності розглядається ![]() - вимірний світ простір-час. Незмінною величиною (інваріантом) в цьому світі є інтервал s, який визначається виразом:
- вимірний світ простір-час. Незмінною величиною (інваріантом) в цьому світі є інтервал s, який визначається виразом:
![]() , (6),
, (6),
де С – швидкість світла,
t – час, що пройшов від однієї події до іншої,
l– відстань між подіями.
Поняття про релятивістську динаміку. Класична механіка як частковий випадок релятивістської механіки
З принципу відносності (всі інерційні системи рівноправні) випливає, що математичний запис будь-якого закону фізики повинна бути однаковою в усіх інерційних системах відліку. Цю умову називають умовою інваріантності фізичних законів відносно перетворень Лоренцо.
Розглянемо основний закон класичної динаміки:
![]() або
або ![]() (7)
(7)
Рівняння (7) інваріантне по відношенню до перетворень Галілея.
Дійсно, ![]() , але
, але ![]() .
.
Тому: ![]() .
.
Але рівняння (7) неінваріантне по відношенню до перетворень Лоренцо (при m=const).Згідно теорії відносності
 (8)
(8)
З урахуванням (8) рівняння (7) залишається інваріантним по відношенню до перетворень Лоренца: