Учебное пособие: Иерархическое управление большими системами

где x, u, xi, ui – имеют размерность n, m, ni, mi, соответственно, а gi – представляет взаимосвязи в i-й подсистеме, и:

(4.3.3)

(4.3.4)

Задачей оптимального управления является поиск управляющих векторов u1,…,uN, таких, что оценочная функция

(4.3.5)

минимизирует объект (4.3.1) и подходящая область:

(4.3.6)

Учитывая возможность декомпозиции системы (4.3.1) на N соединенных подсистем (4.3.2), можно разложить ценовую функцию (4.3.6) и взаимосвязи gi(x,t) (4.3.2), как:

(4.3.7)

(4.3.8)

(4.3.9)

где zi – вектор содержащий линейную (или нелинейную) комбинацию состояний N подсистем. Исходя из описанных предположений, задача оптимального управления большой системой может быть записана как:

(4.3.10)

(4.3.11)

(4.3.12)

(4.3.13)

Эта проблема, известная как иерархическое управление, была решена двухуровневой оптимизацией статистической задачи в предыдущем параграфе. Применение двухуровневого согласования цели для больших линейных систем описано далее.

4.3.1 Двухуровневое согласование линейных систем

Рассмотрим большую линейную стационарную систему:

(4.3.14)

Система может быть декомпозирована как:

(4.3.15)

где вектор взаимодействия (kxl), записанный как:

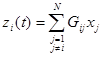(4.3.16)

это линейная комбинация состояний N-1 подсистем, и Gij – это матрица nixnj. Первоначальная задача оптимального управления системой сводится к оптимизации N подсистем, которые удовлетворяют (4.3.15)-(4.3.16) и минимизируют:

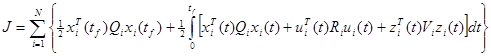(4.3.17)

где Qi – это неотрицательно определенная матрица nixni, Ri и Vi – это положительно определенные матрицы mixmi и kixki , где

(4.3.18)

Физическая интерпретация последнего слагаемого в интеграле (4.3.17) – это неточность в данной точке. Фактически, определяя это слагаемое, как будет видно дальше, мы избегаем выраженных управлений. «Согласование цели» и «баланс взаимодействия» использованные у Mesarvic и др. (1970), так же известны как задача «linear-quadratic» у Pearson (1971) и передача у Singh (1980) и Jamshidi (1983).

В этой декомпозиции большой взаимосвязанной линейной системы общие коэффициенты связи между ее N подсистемами – это переменная взаимосвязи zi(t), которые, вместе с (4.3.15)-(4.3.16), образуют ограничение связи. Эта формулировка называется глобальной и обозначается SG. Можно сделать следующее допущение. Глобальная проблема SG заменяется группой N подзадач, соединенных вместе через вектор параметров a=(a1,…,aN) и обозначенных si(a), i=1,…,N. Другими словами, глобальная системная задача SG включена в группу подсистемных проблем si(a) через внутренний параметр (Sandell и др., 1978) таким образом, что для определенного значения a*, подсистемы Si(a*), и i=1,…,N, дают желаемое решение для SG. Используя обозначения иерархического управления, эта внутренняя идея это и есть понятие согласования, но используя терминологию математического программирования задач, она называется основной проблемой (Geoffrion, 1970). На рисунке 4.6 изображена двухуровневая структура управления большой системой. Под этой стратегией, на i-й итерации каждый местный контроллер i получает от координатора (второй уровень иерархии), решает и передает (сообщает) некоторую функцию этого решения координатору.