Учебное пособие: Иерархическое управление большими системами

где векторы ai(t) и zi(t) – уже не считаются неизвестными на первом уровне, и фактически ai(t) увеличивает zi(t), чтобы образовать широкоразмерный вектор согласования, который мы рассмотрим ниже. Для решения задачи первого уровня, надо принять как известную. Замете, что ui(t) можно выделить из (4.3.43):

(4.3.44)

и подставить в (4.3.40)-(4.3.42), получив:

(4.3.45)

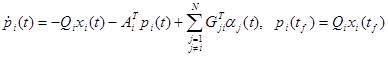(4.3.46)

который образует линейную двухточечную краевую (ДТК) задачу, и, как в (4.3.33) . Можно увидеть, что ДТК задача может быть разложена введением матрицы Риккати. Это выглядит как:

(4.3.47)

где gi(t) – это разомкнутый сопряженный или компенсирующий вектор, размерностью ni. Если обе части уравнения (4.3.47) продифференцированы и и из (4.3.46) и (4.3.45) подставлены в него, можно вновь использовать (4.3.47) и уравнительные коэффициенты для первого и нулевого порядка xi(t), получив следующие матричные и векторные дифференциальные уравнения:

(4.3.48)

(4.3.49)

где конечные условия Ki(tf) и gi(tf) вытекают из (4.3.41) и (4.3.47).

(4.3.50)

В результате данного уравнения оптимальное уравнение первого уровня становится

(4.3.51)

который имеет частичную закрытую обратную связь и прямую (открытую) обратную связь. Можно сделать два вывода. Первый, решение дифференциального, симметричного матричного уравнения Риккати, в которое включены ni(ni+1)/2 нелинейных скалярных уравнений не зависит от первоначального состояния xi(0). Второй, в отличие от Ki(t), gi(t) в (4.3.49) посредством zi(t) зависит от xi(0). Это свойство будет использовано в разделе 4.4, чтобы получить абсолютно закрытое управление в иерархической структуре.

Задача второго уровня сильно изменяет новый вектор согласования . Для этой цели определите аддитивно отделяемый Лагранжиан:

(4.3.52)

Значение ai(t) и zi(t) можно получить из:

(4.3.53)

(4.3.54)

т.е.:

(4.3.55)

Процедура согласования второго уровня на итерации (l+1) имеет вид:

(4.3.56)

Метод прогнозирования взаимодействия формулируется следующим алгоритмом:

Алгоритм 4.2 Метод прогнозирования взаимодействия для непрерывных систем:

Шаг 1. Решить N независимых дифференциальных матричных уравнений Риккати (4.3.48) с конечным условием (4.3.50) и сохраните Ki(t), i=1,2…,N. Инициализируйте ai(t) случайными числами и найдите соответствующее значение для zi(t).

Шаг 2. На l-й итерации используйте значения чтобы решить сопряженное уравнение (4.3.49), с конечным условием (4.3.50). Сохраните gi(t), i=1,2,…,N.

Шаг 3. Решите уравнение состояния