Учебное пособие: Иерархическое управление большими системами

где

Вектор выхода системы представлен как:

(4.3.31)

Необходимо найти стратегию иерархического управления по методу баланса взаимодействий (согласования цели).

Решение: Из схемы системы, показанной на рисунке 4.7 (пунктирные линии) и матрицы состояния (4.3.29) ясно, что есть четыре подсистемы третьего порядка соединенных через шесть ограничивающих уравнений (по числу пунктирных линий на рис. 4.7):

(4.3.32)

где ei, i=1,…,6 представляет ошибки взаимодействия между четырех подсистемами. Задачи подсистем первого уровня были решены через набор из четырех матричных уравнений Риккати третьего порядка:

(4.3.33)

где Ki(t) – это положительно определенная матрица Риккати nixni и . Методы «без взаимодействия» и «удвоения» решают дифференциальное матричное уравнение Риккати, предложены Davison и Maki в 1973 и рассмотрены Jamshidi в 1980,были использованы для компьютерного решения (4.3.33). Уравнения состояния подсистем были решены стандартным методом Рунге-Кутта четвертого порядка, а итерации второго уровня были выполнены по схеме скоростного градиента (4.3.19), (4.3.26)-(4.3.27), используя кубическую сплайн интерполяцию (Hewlett-Packard, 1979) для оценки подходящих численных интегралов. Размер шага был выбран =0.1, как и в более ранних рассмотрениях этого примера (Pearson, 1971; Singh, 1980). Алгоритм скоростного градиента позволил уменьшить ошибку с 1 до за шесть итераций, как показано на рисунке 4.8, который был в тесной связи с результатами предыдущих исследований модифицированной версии системы (4.3.29), полученными Singh (1980). Рассмотрим второй пример.

Пример 4.3.2. Рассмотрим двухколенную модель задачи управления загрязнением реки.

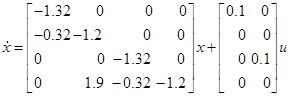(4.3.34)

где каждое колено (подсистема) реки имеет два состояния – x1 – это концентрация биохимической потребности в кислороде (БПК) (биохимическая потребность в кислороде представляет собой уровень содержания кислорода полученного в результате распада органического вещества) и х2 – это концентрация растворенного кислорода (РК) – и управление u1 – это БПК вод втекающих в реку. Для квадратичной функции оценки

(4.3.35)

С Q=diag(2,4,2,4) и R=diag(2,2), необходимо найти оптимальное управление, которое оптимизирует (4.3.35) для объекта (4.3.34) при x(0)=(11 -11)T.

Решение: Как видно из (4.3.34)-(4.3.35), две задачи первого уровня идентичны, и матричное уравнение Риккати второго порядка решается интегрированием (4.3.33) используя метод Рунге-Кутта четвертого порядка при =0.1. Ошибка взаимодействия в этом примере снижена до за 15 итераций, как показано на рисунке 4.9. Оптимальные концентрации БПК и РК двух колен реки показаны на рисунке 4.10.

4.3.2. Метод прогнозирования взаимодействия.

Альтернативный подход к оптимальному управлению иерархическими системами, который имеет как открытый, так и закрытый контур управления, - это метод прогнозирования взаимодействия, который основывается на работе Takahara (1965), который избегает упоминания о градиентных итерациях второго уровня. Рассмотрим большую линейную взаимосвязанную систему, которая декомпозирована на Nподсистем, каждая из которых может быть описана

(4.3.36)

Где вектор взаимодействия zi:

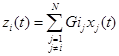(4.3.37)

Задача оптимального управления на первом уровне – найти управление ui(t), которое удовлетворяет (4.3.36)-(4.3.37), минимизируя обычную квадратичную функцию оценки:

(4.3.38)

Эту задачу можно решить введением множества множителей Лагранжа ai(t), и векторов косостояния pi(t), чтобы увеличить ограничение уравнения взаимодействия (4.3.37) и подсистем динамического ограничения (4.3.36) до подынтегральной функции оценки, т.е. Гамильтониан i-й подсистемы будет определен как:

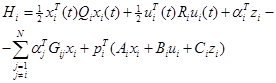(4.3.39)

Затем должно быть написано несколько необходимых условий:

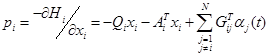(4.3.40)

(4.3.41)

(4.3.42)