откуда

Уравнение адиабатического процесса для газа Ван-дер-Ваальса целесообразно найти из выражения

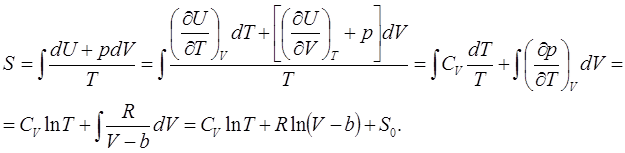
Для получения этого выражения было использовано известное в термодинамике соотношение, которое, также, легко получить с по­мощью якобианов

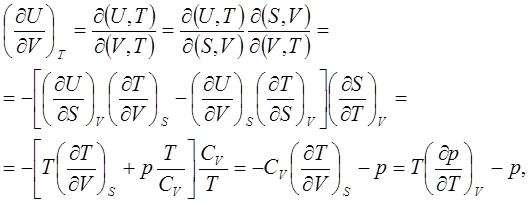(3.1)

гд е использовано соотношение (2.12). Принимая во внимание, что для адиабатического процесса, причём постоянную интегрирования, можно принять равной нулю, получим

или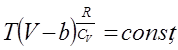

которое для переменных P и V принимает вид:

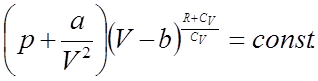
ВЫВОД УРАВНЕНИЯ ДЛЯ ВЫЧИСЛЕНИЯ СКОРОСТИ РАСПРОСТРАНЕНИЯ ЗВУКА В СРЕДЕ.

Найдем выражение для вычисления скорости распространения звука в среде, являющееся адиабатическим процессом.

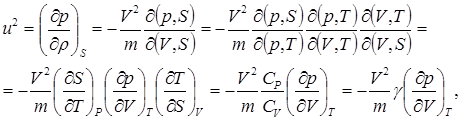
где r – плотность среды, S -энтропия, являющаяся функцией пара­метров P, V и T состояния системы. Этой формулой удобно пользоваться при нахождении скорости звука в газообразн ой среде. В частности, скорос ть звука в воздухе, при норм альн ых условиях можно найти, при мен яя уравнение состоян ия идеального газа, для которого

После подстановки этого выражения в исходную формулу получим:

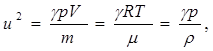
откуда

Подставляя в эту формулу численные значения g , р и r для скорости звука получим U»333 м/с.

Для определения скорости звука в жидких и твёрдых телах необходимо в выражение

подставить значения g , r и из таблиц. Например, для воды U»1400 м/с. Здесь уместно отметить, что скорость звука в морской воде, согласно [5], зависит от температуры, солёнос­ти и гидростатического давления. Необходимо также подчеркнуть, что скорость звука – важная величина, во многом характеризующая физические свойства тел. Зная скорость звука, можно определить упругие постоянные твердых тел, их зависимость от температуры, сжимаемость, отношение теплоемкостей для жидкостей и твердых тел.

СПОСОБ ОПРЕДЕЛЕНИЯ С_V ДЛЯ ИДЕАЛЬНОГО ГАЗА.

Теплое мкость газа при постоянном объёме опре деляется выражением Найдём связь между изменениями внутренней энергии системы и её температуры при постоянном значении р .

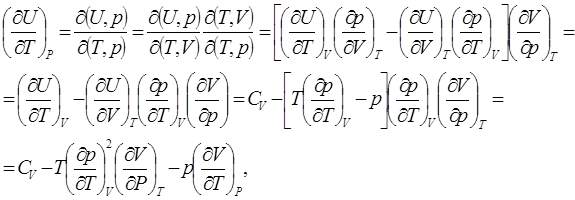(5.1)

где учтены соотношения (3.1) и (2.2).

Найдём также связь между изменениями внутренней энергии системы и её температуры при адиабатическом процессе.

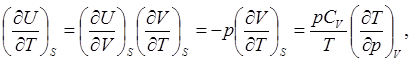(5.2)

где использовано соотношение, объединяющее первое и второе на­чала термодинамики и выражение (2.12).

Отвлекаясь от процессов, протекающих в системе, можно по­казать, что для идеального газа

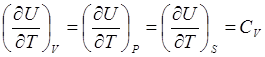
Такое же заключение для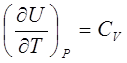,