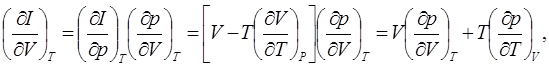(7.10)

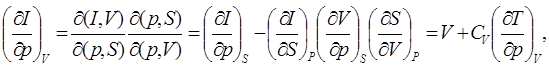(7.11)

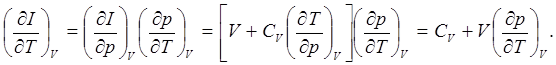(7.12)

Однако это значение частной производной можно определить и бо­лее простым способом, если учесть, что I=U+pV и dI=dU+d(pV). Тогда

Важно подчеркнуть, что одно и то же значение частной про­изводной, при постоянном значении выбранного параметра, можно получить несколькими способами в зависимости от выбора промежу­точных переменных. Учитывая это, при решении задач, можно ввес­ти такие якобианы, тождественно равные единице, которые относи­тельно быстро приведут к цели. Покажем это на одном примере.

a) (7.13)

где были использованы (3.1) и (2.2).

b) (7.14)

Аналогичное значение, но с помощью введения переменных S и p было получено ранее в выражении (6.9).

Приведённый пример показывает, что для проверки правильности нахождения одной и той же термодинамической величины мож­но использовать несколько вариантов, хотя и в данном примере использованы не все.

СПОСОБЫ ОПРЕДЕЛЕНИЯ C_P ДЛЯ ИДЕАЛЬНОГО ГАЗА.

Из объединённого выражения обоих начал термодинамики сле­дует, что если подвод теплоты к системе осуществляется при изо­барическом процессе, то TdS=C_P dT, или

Однако, теплоемкость C_p для идеального газа можно определить как частную производную от тепловой функции по температуре. Действительно, при изобарическом процессе

(8.1)

Это соотношение нетрудно понять, поскольку при р=const

dI=TdS+Vdp=TdS=C_p dT.

Найдём связь между изменениями температуры и тепловой функции при изохорическом процессе.

(8.2)

где учтено выражение (7.11).

В случае адиабатического процесса изменения тех же вели­чин дают:

(8.3)

где использованы соотношения (2.2), (2.8), (7.10) и (8.2).

Непосредственной проверкой нетрудно убедиться, что для идеального газа

(8.4)

Читателям представляется возможность найти удовлетвори­тельное, с точки зрения законов термодинамики, объяснение выражений (8.4).

По аналогии с вышеприведенными примерами, можно решить большое количество задач, связанных со свободной энергией, энтальпией и термодинамическим потенциалом Гиббса.

Вышеприведенные примеры убедительно доказывают преимуще­ство такого подхода к решению задач термодинамики. Этим спосо­бом, в основном, решаются и задачи, связанные с термодинамикой стержней, диэлектриков и магнетиков, примеры которых приведены в [4] и [7], для которых можно учесть электро- и магнитострикционные явления, пьезоэлектрический и пьезомагнитный эффекты, а также и задачи, связанные с химическим потенциалом, когда количество вещества в системе изменяется .

Применение якобианов, особенно после изучения свойств термодинамических функций и их дифференциалов, позволяет более доступным способом решить ту или иную задачу, и, что очень важ­но, даёт возможность, даже при решении одной задачи, охватывать большой материал, предусмотренный программой. Преимущество та­кого подхода к рассмотрению отдельных, или группы, вопросов, как показали наши наблюдения, не вызывает сомнений как с точки зрения корректности математических выражений, так и логичности и взаимосвязи явлений термодинамики.

СОСТАВЛЕНИЕ ДЕТЕРМИНАНТОВ ЯКОБИ И ТАБЛИЦЫ ТЕРМОДИНАМИЧЕСКИХ КОЭФФИЦИЕНТОВ ДЛЯ СИСТЕМ, ОПИСЫВАЕМЫХ БОЛЬШИМ ЧИСЛОМ ПЕРЕМЕННЫХ.

В качестве примера рассмотрим систему, описываемую тремя независимыми переменными, например, систему с переменным коли­чеством вещества. В этом случае дифференциалы термодинамических функций имеют вид:

dU=TdS-pdV+mdN, (9.1)