Учебное пособие: Математический анализ. Практикум

Определение 1. Функция называется первообразной для , если .

Определение 2. Неопределенным интегралом от функции f(x) называется совокупность всех первообразных для этой функции.

Обозначение: , где c- произвольная постоянная.

Свойства неопределенного интеграла

1. Производная неопределенного интеграла:

2. Дифференциал неопределенного интеграла:

3. Неопределенный интеграл от дифференциала:

4. Неопределенный интеграл от суммы (разности) двух функций:

;

5. Вынесение постоянного множителя за знак неопределенного интеграла:

3.1.2 Таблица интегралов

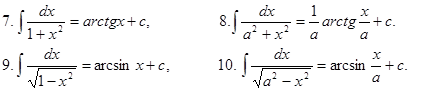
3 .1.3 Основные методы интегрирования

1. Использование свойств неопределенного интеграла.

Пример 29.

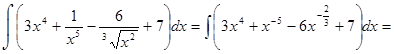
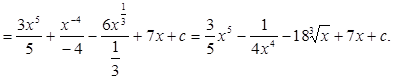
2. Подведение под знак дифференциала.

Пример 30.

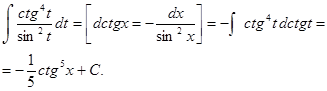
3. Метод замены переменной:

а) замена в интеграле

:

,

где - функция, интегрируемая легче, чем исходная; - функция, обратная функции ; - первообразная функции .

Пример 31.