Учебное пособие: Математический анализ. Практикум

– вертикальная асимптота при , т.к.

– наклонных асимптот нет

, – горизонтальная асимптота

3) – функция убывает на каждом из промежутков.

Схематичный график данной функции:

2.4.3 Наибольшее и наименьшее значение функции на отрезке

Чтобы найти наибольшее и наименьшее значение функции на отрезке можно воспользоваться схемой:

1. Найти производную функции .

2. Найти критические точки функции, в которых или не существует.

3. Найти значение функции в критических точках, принадлежащих заданному отрезку и на его концах и выбрать из них наибольшее и наименьшее .

Пример. Найти наименьшее и наибольшее значение функции на данном отрезке.

25. на промежутке

1)

2) – критические точки

3) ,

–

–

26. на промежутке .

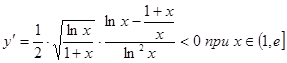
Производная не существует при , но 1 не принадлежит данному промежутку. Функция убывает на промежутке , значит, наибольшего значения нет, а наименьшее значение .

2.5 Правило Лопиталя

Теорема. Предел отношения двух бесконечно малых или бесконечно больших функций равен пределу отношения их производных (конечному или бесконечному), если последний существует в указанном смысле.

Т.е. при раскрытии неопределенностей вида или можно использовать формулу:

.

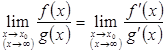Примеры.

27.

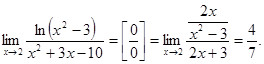
28.