Учебное пособие: Математическое моделирование и расчет систем управления техническими объектами

Зная передаточную функцию и изображение переменной входа, легко найти изображение выхода

Y (s ) = W (s )F (s ).

Пример. Пусть система описывается дифференциальным уравнением второго порядка:

Преобразуем это уравнение по Лапласу, для чего воспользуемся свойством линейности оператора преобразования L , а также теоремой о дифференцировании оригинала:

a ₂ (s ² Y (s ) – sy (0) – y ¢(0)) + a ₁ (sY (s ) – y (0)) + a ₀ Y (s ) = b ₀ F (s ).

Последнее уравнение перепишем в следующем виде:

(a ₂ s ² + a ₁ s + a ₀ )Y (s ) = b ₀ F (s ) + a ₂ sy (0) + a ₂ y '(0) + a ₁ y (0).

При нулевых начальных условиях y (0) = y '(0) = 0 отношение изображений, т.е. передаточная функция

Оператор, связывающий вход и выход, можно задать коэффициентом и множествами нулей (корней полинома) z_j ; j = 1, …, m и полюсов (корней полинома знаменателя) p_i ; i = 1, …, n. Передаточная функция будет равна:

(4)

В отличие от полиномиальной формы (3) форму задания передаточных функций (4) иногда называют факторизованной.

Вводится понятие структуры оператора преобразования. Для дифференциального уравнения n -го порядка (1) и передаточной функции (3) задание структуры означает задание целых чисел – степеней n = deg A и m = deg B – полиномов А и В .

Параметрамиоператора являются коэффициенты полиномов.

Временные характеристики являются одной из форм представления операторов преобразования переменной f (t ) в переменную y (t ). Импульсная переходная функция, или функция веса w (t ) – реакция системы на единичный идеальный импульс (рис.4, а ) при нулевых начальных условиях. переменная выхода определяется как интеграл свертки:

(5)

т.е. в этом случае оператор преобразования имеет форму интегрального уравнения.

Другая часто употребляемая временная характеристика – переходная (рис.4, б ) характеристика h (t ) – реакция системы на единичную ступенчатую функцию1(t ) при нулевых начальных условиях. На рис.4 приведен примерный вид временных характеристик для системы второго порядка.

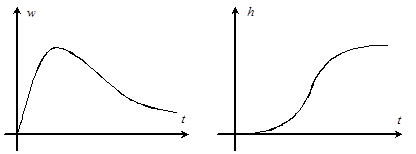
Частотные характеристики элементов и систем представляют собой зависимость параметров установившихся реакций на гармонические сигналы всех частот и единичных амплитуд. В линейных системах форма и частота установившейся реакции совпадают с входом. Комплексная частотная характеристика W ( ) дает возможность определить амплитуду и фазу гармонического сигнала на выходе системы по значению частоты:

(6)

где и j(w)== argW (j w) – амплитудная и фазовая частотные характеристики; , и – вещественная и мнимая частотные характеристики.

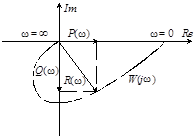
На рис.5. изображен пример годографа W , называемого амплитудно-фазовой характеристикой (АФХ). Реальные объекты с повышением частоты хуже пропускают сигналы – ослабляют амплитуду и вносят отрицательный фазовый сдвиг.

Амплитудно-частотные характеристики удобно представлять в логарифмическом масштабе: Если частота изменяется в логарифмическом масштабе, то логарифмические амплитудно-частотные характеристики (ЛАЧХ) во многих практически важных случаях мало отличаются от прямолинейных асимптот с наклонами, кратными 20 дБ/дек. На рис.6 приведен примерный вид асимптотической ЛАЧХ; штриховая кривая – точная ЛАЧХ. Там же указаны наклоны асимптот в децибелах на декаду.

Хотя за основу задания динамических свойств систем может быть принята любая из форм представления операторов, для конкретных исследований та или иная форма оказывается более рациональной и возникает необходимость перехода от одной формы к другой. Многие задачи анализа связаны с преобразованием формы представления оператора. В ряде случаев эта процедура составляет наиболее трудоемкий этап анализа – построение частной модели, т.е. приведение к форме, позволяющей непосредственно вычислить показатели качества и вывести суждение о соответствии поведения системы заданным требованиям (например, построение временных или частотных характеристик системы управления).

Наиболее прост формальный переход путем замены оператора дифференцирования на комплексный аргумент s от дифференциального уравнения (2) к передаточной функции (3) и обратно. Осуществляя переход к передаточным функциям, следует избегать сокращения общих делителей полиномов числителей и знаменателей, т.е. диполей рациональных функций. Такое сокращение при водит к потере части собственных составляющих движения при ненулевых предначальных условиях (составляющих свободных движений).