Учебное пособие: Методические указания по выполнению курсовой работы Составитель : Пономарев Б. Б. Иркутск, 1995 г

BM=2r₃ ; AB=r₂ =0,847м; j₁ (0)=1,63рад; j₂ (0)=3,37рад;

j₃ (0)=2,87рад; CP=0,5r₃ ; V₁ =4,5м/c; a=0,02рад;

t=0,48c; Dt=0.02c; p=13,08c^-1 .

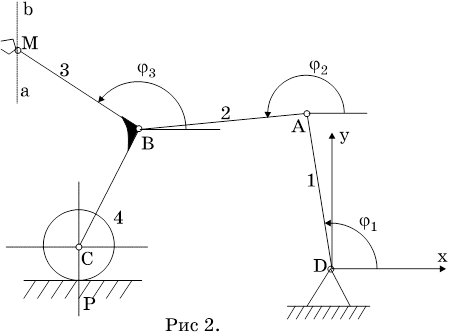
2. Составление уравнений движения . Составляются уравнения для четырех неизвестных угловых скоростей звеньев w_1z , w_2z , w_3z , w_4z . При заданном движении точки М они определяются из уравнений внешних связей, налагаемых на механизм. На данный механизм наложены связи: V_Dx =0, V_Dy =0, V_px =0, V_py =0, V_cy =0. (5)

При вычислении скорости точки С последовательно определяются скорости точек в соответствии с графом МВС,при вычислении скорости точки Р - в соответствии с графом МВСР,при вычислении скорости точки D₄ - в соответствии с графом МВАD или РСВАD или СВАD.

Составляются все возможные варианты векторных уравнений

(6)

(7)

(8)

(9)

(10)

Проецируя обе части уравнений на оси координат X и Y с учетом (5) получим систему алгебраических уравнений для определения w_iz (i=1,2,3,4). Уравнение (6) проецируется на ось Y, так как V_cy =0, то

V_my +w_3z ´2r₃ ´cos(j₃ +p)+w_3z ´r₃ ´сos(j₃ +)=0 (11)

Уравнение (7) проецируется на оси X и Y, так как V_px =0 и V_py =0, то

0 - w_3z ´2r₃ ´sin(j₃ +p) - w_3z ´r₃ ´sin(j₃ +) - w_4z ´0,5r₃ ´sinp=0 (12)

V_My + w_3z ´2r₃ ´cos(j₃ +p) + w_3z ´r₃ ´cos(j₃ +) + w_4z ´0,5r₃ ´cosp=0 (13)

Уравнение (8) проецируется на оси X и Y, так как. V_Dx =0 и V_Dy =0, то

0 - w_3z ´2r₃ ´sin(j₃ +p) - w_2z ´r₂ ´sin(j₂ -p) - w_1z ´r₁ ´sin(j₁ +p)=0 (14)

V_my + w_3z ´2r₃ ´cos(j₃ +p) + w_2z ´r₂ ´cos(j₂ -p) + w_1z ´r₁ ´cos(j₁ +p)=0 (15)

Уравнение (9) проецируется на оси X и Y, так как

V_Dx =0, V_Oy =0, V_Px -0, V_Py =0, то

- w_4z ´0.5r₃ ´sin - w_3z ´r₃ ´sin(j₃ - ) - w_2z ´r₂ ´sin(j₂ - p)-w_1z ´r₁ ´sin(j₁ +p)=0

(16)

w_4z ´0.5r₃ ´cos+w_3z ´r₃ ´cos(j₃ - )+w_2z ´r₂ ´cos(j₂ - p)+w_1z ´r₁ ´cos(j₁ +p)=0

(17)

Уравнение (10) проецируется на ось Y, так как V_Dx =0, V_Dy =0 и V_Cy =0, то

w_3z ´r₃ ´cos(j₃ -)+ w_2z ´r₂ ´cos(j₂ -p) + w_1z ´r₁ ´cos(j₁ +p)=0 (18)

Из составленных уравнений связей выбираем 4, позволяющих наиболее простым путем произвести преобразования и выразить одни неизвестные через другие. В данном случае это уравнения (11), (12), (16), (18), которые с учетом формул приведения запишутся в следующем виде:

« 9 10 11 12 13 14 15 16 17 18 » К-во Просмотров: 1318 Бесплатно скачать Учебное пособие: Методические указания по выполнению курсовой работы Составитель : Пономарев Б. Б. Иркутск, 1995 г >>> Скачать <<< Меню Поиск