Учебное пособие: Методические указания по выполнению курсовой работы Составитель : Пономарев Б. Б. Иркутск, 1995 г
Из уравнений (37) , (38) получают:
w3z =VMy /[r3 (2cosj3 +sinj3 )];
Vcx =VMx +w3z ´r3 (2sinj3 - cosj3 ); (39)
w1z =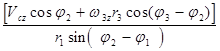
;
w2z =
.
Уравнения (39) дополним дифференциальными соотношениями
; 
; 
(40)
3. Определение параметра управления . Из (34) и (35) получим уравнение в рассогласованиях:
T* 
Dx+Dx=0; T* Dy+Dy=0.
Решение этих уравнений имеет вид:
Dx=Dx(0) e- 
, Dy=Dy(0) e- ,
По условию, при t=t2 должно выполняться соотношение
d = 
=0,01. Отсюда
Т* = 
=0,297 c.
4. Решение задачи и обработка результатов . Система уравнений (36), (39), (40) интегрируется с помощью ЭВМ на интервале [0; 1,37] с использованием конечноразностной схемы Эйлера. Шаг интегрирования Dt=0,057c.
Начальные условия по переменным j1, j2 , j3 (рис.4) приведены в исходных данных, а по переменным XM, YM вычисляются по формулам :
XM =r1 ´cosj1 +r2 ´cosj2 +2r3 ´cosj3 (41)
YM =r1 ´sinj1 +r2 ´sinj2 +2r3 ´sinj3
Подставив в (41) числовые значения ri , ji (0), получают XM (0), YM (0). Последующие шаги интегрирования осуществляются с использованием зависимостей (22), с учетом, что
=XM (k) +VMx (k) ´Dt;
=YM (k) +VMy (k) ´Dt, (42)
с использованием зависимостей (41)
Результаты счета по двум вариантам сравниваются.
Программа счета составляется на любом языке программирования,результаты оформляются в виде таблицы. По результатам решения строятся графики j1 (t), w1z (t), Vcx (t) и траектории сближения точек М и К, которые не должны иметь разрывов,а координаты точек М и К в момент времени t должны быть достаточно близки.
Графоаналитическая проверка результатов счета производится аналогично проверке в первой задаче.
III. Динамика механизма с двумя степенями свободы .
Описание задания .
Манипулятор с двумя степенями свободы (рис.1) переносит точечный груз М массой m за время t3 под действием двигателей управления, расположенных в шарнирах B и D из точки d в точку е с заданной скоростью
VMx =0, VMy =V3 sinkt (43)