Учебное пособие: Методические указания по выполнению курсовой работы Составитель : Пономарев Б. Б. Иркутск, 1995 г

_M =V_Mx (X_M ,t); _M =V_My (Y_M ,t); (31)

_i =w_iz (j_i , V_mx , V_my , t) (i=1,2,3)

Эти уравнения манипулятора,являющегося системой с двумя степенями свободы, записаны в избыточном наборе пяти переменных X_M , Y_M , j₁ , j₂ , j₃ . Отсюда следует, что из начальных значений этих переменных независимо могут задаваться только два. В таблице 1 независимыми задаются величины j₁ (0), j₂ (0), значения j₃ (0) указанные в таблице,вычислены по j₁ (0), j₂ (0) для рассматриеваемой конструктивной схемы манипулятора. Значения X_M (0), Y_M (0) следует находить по заданным j₁ (0), j₂ (0), j₃ (0).

Указания к решению задачи. Дифференциальные уравнения движения манипулятора с заданными начальными условиями интегрируются на интервале времени [ 0, t₂ ] с шагом Dt. При решении задачи рекомендуется использовать конечноразностную схему Эйлера.

Контроль решения. Построенные по результатам счета графики не должны иметь разрывов. При t=t₂ рассогласование между точками М и К должно быть величиной порядка d от начального. Результаты вычисления на ЭВМ для момента времени t=(N+1)´Dt угловых скоростей звеньев и скорости точки С должны совпадать с результатами графоаналитического решения для этого момента времени. Расхождения не должны превышать 5%.

Пример выполнения задания .

(вариант 31, n=1, N=2)

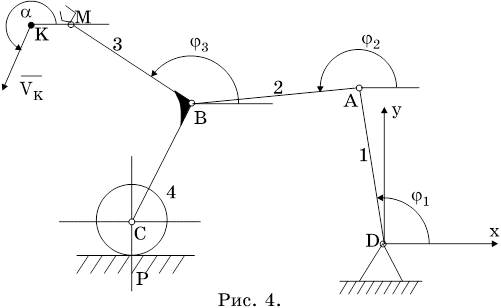
1. Постановка задачи. Управление манипулятором (рис.4) должно обеспечить за время t₂ сближение захвата М с движущейся деталью К. Деталь движется прямолинейно с постоянной скоростью V_к в указанном на рисунке направлении. Начальное положение манипулятора задано углами поворота звеньев j₁ (0), j₂ (0), j₃ (0). К моменту времени t=t₂ требуется относительная точность d совмещения точек М и К. Управление манипулятором осуществляется по линейной комбинации рассогласований и их производных.

Дано: V_k =0,304м/c; a=4,35рад; DA=r₁ =0,953м; BC=r₃ =0,457м; BM=2r₃ ; AB=r₂ =0,847м; j₁ (0)=1.63рад; j₂ (0)=3,37рад; j₃ (0)=2,87рад; X_k (0)=-2,16м; Y_k =1,18м; d=0,01; t₂ =1,37c; Dt=0,057c.

Требуется: 1. Составить уравнения управляемого движения точки М, уравнения углового движения звеньев манипулятора и уравнения для скорости точки С. 2. Выбрать параметры управления, обеспечивающего сближение точек М и К с заданной точностью. 3. Проинтегрировать с помощью ЭВМ уравнения движения на интервале времени [ 0, t₂ ]. 4. Построить траектории сближения точек М и К и графики j₁ (t), w_1z (t), V_cx (t). 5. Для момента времени t=(N+1)Dt=0,456c провести графоаналитическое решение задачи и сравнить с результатами счета.

2. Составление уравнений движения. Уравнения движения детали К имеют вид:

X_k =X_k (0)+V_kx ´t; V_kx =V_k cosa= - 0,108м/c; (32)

Y_k =Y_k (0)+V_ky ´t; V_ky =V_k sina= - 0,284м/c.

Предполагая,что координаты захвата М известны в процессе движения,можно вычислить рассогласования координат точек К и М.

DX=X_k - X_M; DY=Y_k - Y_M (33)

Учитывая,что управление манипулятором осуществляется по линейной комбинации рассогласовании и их производных

u_x =DX + T^* DX; u_y =DY + T^* DY (34)

При управлении с большими коэффициентами усиления k с погрешностью порядка 1/k выполняются соотношения:

u_x =0, u_y =0. (35)

Подставляя (35) в выражения (32), (33), (34) и приводя полученные уравнения к форме Коши получаем:

=V_Mx ; V_Mx =V_kx + [X_k (0) + V_kx ´t - X_M ] / T^* ;

=V_My ; V_My =V_ky + [Y_k (0) + V_ky ´t - Y_M ]/T^* . (36)

Угловое движение звеньев манипулятора и скорость точки С однозначно определяется движением точки М и внешними связями, налагаемыми в точках D и С. Составляются выражения для проекций скоростей точек С и М.

В соответствии с графом СВМ запишем:

V_Mx =V_cx - w_3z ´r₃ ´sin(j₃ - ) - w_3z ´2r₃ ´sinj₃ ;

V_my =w_3z ´r₃ ´cos(j₃ - ) + w_3z ´2r₃ ´cosj₃ ; (37)

В соответствии с графом DABC

V_cx = - w_1z ´r₁ ´sinj₁ - w_2z ´r₂ ´sinj₂ - w_3z ´r₃ ´sin(j₃ + ); (38)