Учебное пособие: Методы компьютерных вычислений и их приложение к физическим задачам 2

Вычислим …=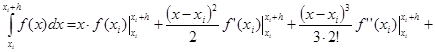

==

Получили формулу правых (или левых) прямоугольников и априорную оценку погрешности r на отдельном шаге интегрирования. Основной критерий, по которому судят о точности алгоритма – степень при величине шага в формуле априорной оценки погрешности.

В случае равного шага h на всем диапазоне интегрирования общая формула имеет вид

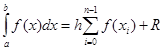
Здесь n – число разбиений интервала интегрирования

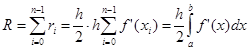
Для справедливости существования этой оценки необходимо существование непрерывной f’(x).

Метод средних прямоугольников. Здесь на каждом интервале значение функции считается в точке

, то есть

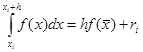
Разложение функции в ряд Тейлора показывает, что в случае средних прямоугольников точность метода существенно выше:

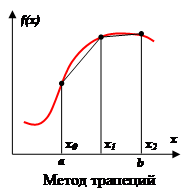
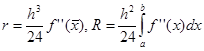
Метод трапеций.

Аппроксимация в этом методе осуществляется полиномом первой степени. Суть метода ясна из рисунка.

На единичном интервале.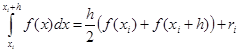

В случае равномерной сетки (h = const)

При этом , а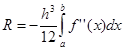

Погрешность метода трапеций в два раза выше, чем у метода средних прямоугольников! Однако на практике найти среднее значение на элементарном интервале можно только у функций, заданных аналитически (а не таблично), поэтому использовать метод средних прямоугольников удается далеко не всегда. В силу разных знаков погрешности в формулах трапеций и средних прямоугольников истинное значение интеграла обычно лежит между двумя этими оценками.

Особенности поведения погрешности.

Казалось бы, зачем анализировать разные методы интегрирования, если мы можем достичь высокой точности, просто уменьшая величину шага интегрирования. Однако рассмотрим график поведения апостериорной погрешности R результатов численного расчета в зависимости от числа n разбиений интервала (то есть при шаг ). На участке (1) погрешность уменьшается в связи с уменьшением шага h. Но на участке (2) начинает доминировать вычислительная погрешность, накапливающаяся в результате многочисленных арифметических действий. Таким образом, для каждого метода существует своя R_min , которая зависит от многих факторов, но прежде всего от априорного значения погрешности метода R.

Уточняющая формула Ромберга.

Метод Ромберга заключается в последовательном уточнении значения интеграла при кратном увеличении числа разбиений. В качестве базовой может быть взята формула трапеций с равномерным шагом h.

Обозначим интеграл с числом разбиений n = 1 как

Уменьшив шаг в два раза, получим