Учебное пособие: Методы компьютерных вычислений и их приложение к физическим задачам 2
Простейшим итерационным методом решения СЛАУ является метод простой итерации. При этом система уравнений 
(1) преобразуется к виду
(2)
а ее решение находится как предел последовательности
(3)
где {n} – номер итерации. Утверждается, что всякая система (2), эквивалентная (1), записывается в виде
Теорема о достаточном условии сходимости метода простой итерации утверждает, что если норма матрицы
(
)
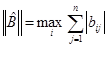то система уравнений (2) имеет единственное решение и итерационный процесс (3) сходится к решению со скоростью геометрической прогрессии.
Теорема о необходимом и достаточном условии сходимости метода простой итерации: Пусть система (2) имеет единственное решение. Итерационный процесс (3) сходится к решению системы (2) при любом начальном приближении тогда и только тогда, когда все собственные значения матрицы 
по модулю меньше 1.
На практике для обеспечения сходимости итерационных методов необходимо, чтобы значения диагональных элементов матрицы СЛАУ были преобладающими по абсолютной величине по сравнению с другими элементами.
Представим СЛАУ в следующей форме, удовлетворяющей (3):
