Учебное пособие: Методы компьютерных вычислений и их приложение к физическим задачам 2

Пусть мы вычислили четыре раза интеграл с n от 1 до 4. Представим следующий треугольник:

R(1;1)

R(2;1) R(2;2)

R(3;1) R(3;2) R(3;3)

R(4;1) R(4;2) R(4;3) R(4;4)

В первом столбце стоят значения интеграла, полученные при последовательном удвоении числа интервалов. Следующие столбцы – результаты уточнения значения интеграла по следующей рекуррентной формуле:

.

Правое нижнее значение в треугольнике – искомое уточненное значение интеграла.

Метод Симпсона.

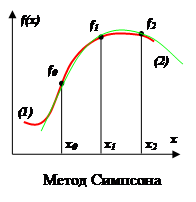
Подинтегральная функция f(x) заменяется интерполяционным полиномом второй степени P(x) – параболой, проходящей через три узла, например, как показано на рисунке ((1) – функция, (2) – полином).

Рассмотрим два шага интегрирования (h = const = x_{i +1} – x_i ), то есть три узла x₀ , x₁ , x₂ , через которые проведем параболу, воспользовавшись уравнением Ньютона:

.

Пусть z = x – x₀ ,

тогда

Теперь, воспользовавшись полученным соотношением, сосчитаем интеграл по данному интервалу:

В итоге .

Для равномерной сетки и четного числа шагов n формула Симпсона принимает вид:

Здесь , а

В предположении непрерывности четвертой производной подинтегральной функции.

Блок-схема алгоритма метода Симпсона

Методы Монте-Карло