Учебное пособие: Понятие многомерной случайной величины

Рис. 1. Кривые плотности нормального распределения с различными а и λ

Изменение среднего квадратического отклонения при фиксированном значении математического ожидания приводит к изменению формы кривой распределения. С уменьшением λ вершина кривой распределения будет подниматься, кривая будет более «островершинной» (вытянутой вдоль оси симметрии). С увеличением λ кривая распределения менее островершинная и более растянута вдоль оси абсцисс. Одновременное изменение параметров a и λ приведет к изменениюи формы, и положения кривой нормального распределения.

Условимся о форме записи случайных величин. Например, запись X~а (X; М(Х), σ² ) означает: случайная величина X подчиняется закону распределения а с математическим ожиданием М(Х) и средним квадратическим отклонением σ, либо дисперсией σ² . Это общая форма записи случайной величины, распределенной по закону а. Если речь идет о биномиальном законе, то будем обозначать В; о нормальном – N и т.д.

Итак, если мы имеем дело со случайной величиной, подчиняющейся нормальному закону распределения, с математическим ожиданием а = 5,7 и λ = 2, то запись будет X~N (X; 5,7; 2² ).λ² записывается как 2² , а не 4.

Стандартное (нормированное) нормальное распределение

Если вформуле (1) а = 0; λ = 1, то

φ(z) = 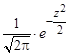. (2)

При а = 0 и λ = 1 нормальное распределение называют стандартным (нормированным) нормальным распределением (рис. 2), а кривую – нормированной.

λ = 1

??????????? ?????????? ????????? ???????? ???????????? Z. ??????? ?? ?????????????? ???????: Z~N (z; 0,1² ). ????????????? φ(z) ????????????.

Свойства функции φ(z):

а) функция φ(z) – четная, т.е.

φ(z) = φ(– z);

б) с увеличением z по абсолютной величине φ(z) монотонно убывает и при z → ∞ имеет пределом нуль;

в) при z = 4 φ(z) = 0,0001, при z = 5 φ(z) = 0,0000015, поэтому при |z | > 5 можно считать, что φ(z) = 0. В связи с этим таблицы ограничиваются значениями функции φ(z) для аргументов z = 4 или z = 5;

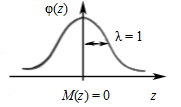
Рис. 2. График кривой стандартного нормального распределения

г) максимальное значение функция φ(z) принимает при z = 0.

Сравнивая (1) и (2), можно сделать вывод: плотность случайной величины, распределенной по нормальному закону, можно записать как:

W(x) =. (3)

Любая нормально распределенная случайная величина может быть преобразована в стандартную (нормированную) нормально распределенную случайную величину.

Итак, переход X в Z достигается преобразованием:

Z = (x – a)/λ. (4)

При помощи формулы (6.4) можно преобразовать любую нормально распределенную случайную величину X в стандартную нормально распределенную случайную величину Z. Обратное преобразование стандартной нормальной случайной величины Z в Х~N (Х; a; λ² ) можно осуществить по формуле:

X = a+Z∙λ. (5)

Вероятность попадания в заданный интервал нормально распределенной случайной величины.

Мы знаем, что если случайная величина задана плотностью распределения W(x), то вероятность того, что X примет значение, принадлежащее интервалу (α, b), определяется из выражения

.

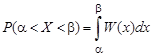Если случайная величина X ~ N (a; σ² ), то

P(a<X<b) = 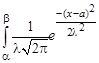dx.

Для того чтобы можно было пользоваться готовыми таблицами для вычисления вероятностей, преобразуем X в Z и найдем новые пределы интегрирования. Если х = a, то z=(a–а)/λ, если х=b, то z= (b – а)/λ. Тогда P (a< X<b) = 1/(λ),