где x = a + zλ; dx = λdz.

Интеграл вида 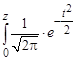dt называется интегралом вероятностей, или функцией Лапласа. Его обычно обозначают символом F₀ (z):

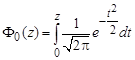(6)

Интеграл Лапласа в общем виде не берется. Его можно вычислить одним из способов приближенного вычисления интегралов. Эта функция табулирована. Пользуясь функцией Лапласа, окончательно получаем:

P (a<X <b) = . (7)

Формула (7) называется интегральной теоремой Лапласа.

Свойства F₀ (z):

а) функция F₀ (z) является нечетной функцией; т.е. F₀ (–z)= –F₀ (z);

б) при z = 0 функция Лапласа равна нулю 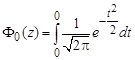=0;

в) при z®+∞F₀ (z)®0,5; при z® –∞ F₀ (z)® –0,5.

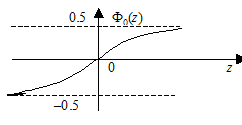
Рис. 4. График интегральной функции Лапласа–Гаусса

Ф₀ (4) = 0,499997, Ф₀ (–4) = –0,499997. Значит, при úzú> 4 можно считать, что Ф₀ (4) » ± 0,5. Итак, все возможные значения интегральной функции Лапласа принадлежат интервалу (–0,5; +0,5).

Итак, функция распределения случайной величины, подчиняющейся нормальному закону распределения, представленная через функцию Лапласа,

F(x) = 0,5+Ф_о [(x – a)/λ]. (8)

Рассмотрим ряд примеров на вычисление вероятностей при помощи таблиц стандартного нормального распределения и нахождение значений Z по заданной вероятности.

Правило «трех сигм»

Если обозначить (x–a)/σ = Z, Δ = (x – a) = σZ, то

P (|X – a| < z) = 2Ф₀ (z), (9)

где 2Ф₀ (z) – вероятность того, что отклонение случайной величины от ее математического ожидания М(Х)= а по абсолютной величине будет меньше z сигм. Придадим z значения 1; 2; 3. Пользуясь формулой (9) и таблицей интеграла вероятностей, вычислим вероятность того, что отклонение по абсолютной величине будет меньше σ, 2σ и Зσ:

при z =1, Δ = σ и P (|X–a|<σ) = 2Ф₀ (1) = 0,6826;

при z =1, Δ =2σ и P (|X–a|<2σ) = 2Ф₀ (2) = 0,9544

при z =1, Δ =3σ и P (|X–a|< 3σ) = 2Ф₀ (3) = 0,9973.

Приведенные результаты вычислений представлены на рис. 5.

Вероятность того, что случайная величина попадет в интервал (а – σ; а + σ), равна 0,6826. Геометрически эту вероятность можно представить заштрихованной частью площади под кривой, изображенной на рис. 8. Вероятность того, что случайная величина попадет в интервал (а – 2σ; а +2σ), равна 0,9544. Вероятность того, что случайная величина попадет в интервал (а – 3σ; а +3), равна 0,9973 (на рис. 8 эта вероятность представлена почти всей площадью, заключенной между кривой распределения и осью абсцисс).

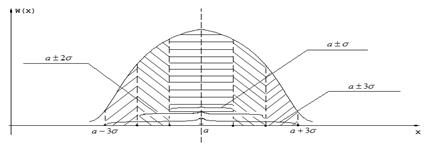
Рис. 5. К правилу «трех сигм»

Следовательно, вероятность того, что отклонение случайной величины от своего математического ожидания по абсолютной величине превысит утроенное среднее квадратическое отклонение, очень мала и равна 0,0027. Такие события считаются практически невозможными.

В этом и состоит правило «трех сигм»: если случайная величина распределена по нормальному закону, то ее отклонение от математического ожидания практически не превышает±3σ.

Понятие о теоремах, относящихся к группе «центральной предельной теоремы»