Учебное пособие: Понятие многомерной случайной величины

Центральная предельная теорема для одинаково распределенных слагаемых (П. Леви). Если независимые случайные величины Х₁ , Х₂ ,… Х_n , имеют один и тот же закон распределения с математическим ожиданием а и дисперсией σ² , то при неограниченном увеличении n закон распределения суммы Х₁ + Х₂ + … + Х_n неограниченно приближается к нормальному.

Теорема Ляпунова. Если случайная величина Y представляет собой сумму большого числа независимых случайных величин Y₁ , Y₂ ,… Y_n , влияние каждой из которых на всю сумму равномерно мало, то величина Y имеет распределение, близкое к нормальному, и тем ближе, чем больше п.

При этом ценно то, что законы распределения суммируемых случайных величин могут быть любыми, заранее не известными исследователю. Практически данной теоремой можно пользоваться и тогда, когда речь идет о сумме сравнительно небольшого числа случайных величин. Опыт показывает, что при числе слагаемых около 10 закон распределения суммы близок к нормальному.

Теорема Ляпунова имеет важное практическое значение, поскольку многие случайные величины можно рассматривать как сумму отдельных независимых слагаемых. Например: ошибки различных измерений; отклонения размеров деталей, изготовляемых при неизменном технологическом режиме; распределение числа продаж некоторого товара, объемов прибыли от реализации однородного товара различными производителями; валютные курсы; рост, вес животных и растений данного вида; отклонение точки падения снаряда от цели и т.д. могут рассматриваться как суммарный результат большого числа слагаемых и потому приближенно следовать нормальному закону распределения.

Показательное (экспоненциальное) распределение

Экспоненциальное (показательное) распределение тесно связано с распределением Пуассона, которое используется для вычисления вероятности появления события в некоторый период времени. Распределение Пуассона – это распределение числа появления событий в заданный интервал времени длиной t. Единственный параметр распределения Пуассона λ характеризует интенсивность процесса, т.е. с его помощью мы можем вычислить среднее число появления события.

Закон равномерного распределения (равномерной плотности)

Если возможные значения непрерывной случайной величины принадлежат определенному интервалу, а плотность ее распределения на этом интервале остается постоянной, то говорят, что данная случайная величина распределена по закону равномерной плотности.

В равномерном распределении вероятность того, что случайная величина будет принимать значения внутри заданного интервала, пропорциональна длине этого интервала.

Пусть непрерывная случайная величина X распределена на интервале (α, β) с равномерной плотностью. Ее плотность W(х) на этом участке постоянна и равна C. Вне этого интервала она равна нулю, так как случайная величина X за пределами интервала (α, β) значений не имеет (рис. 6).

Рис. 6. Общий вид графика функции плотности равномерного распределения

Найдем значение постоянной С. Площадь, ограниченная кривой распределения и осью абсцисс, должна быть равна единице, т.е. С (β – α) = 1. Следовательно, С = 1/(β – α) и плотность для равномерного распределения можно записать:

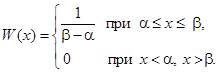(10) Функция распределения

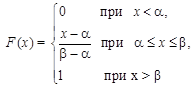(11)

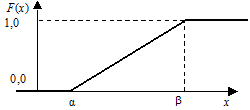
Рис. 7. График функции распределения для случайной величины, распределенной по закону равномерной плотности

Математическое ожидание непрерывной равномерно распределенной случайной величины

М(Х)= (α + β)/2, (12)

дисперсия D(x) = (β –α)² /12, (13)

среднеквадратичное отклонение

s(x) = = (β – α) / (2). (14)

Для непрерывной равномерно распределенной случайной величины X, заданной на интервале

(a<X<b), P (a<X<b) = (b–a)/(β – α), (15)

если .

Литература: [2], [4], [5].

Литература

1. Высшая математика для экономистов: Учебник для вузов / Под ред. Н.Ш. Кремера. – М.: ЮНИТИ, 2003.

2.Е.С. Кочетков, С.О. Смерчинская Теория вероятностей в задачах и упражнениях / М. ИНФРА-М 2005.