Учебное пособие: Цилиндр

Сечение цилиндра плоскостью, параллельной его оси, представляет собой прямоугольник (рис. 3, а). Две его стороны − образующие цилиндра, а две другие − параллельные хорды оснований.

а)б)

в) г)

Рис. 3 – Сечения цилиндра

В частности, прямоугольником является осевое сечение. Это − сечение цилиндра плоскостью, проходящей через его ось (рис. 3, б).

Сечение цилиндра плоскостью, параллельной основанию − круг (рис 3, в).

Сечение цилиндра плоскостью не параллельной основанию и его оси − овал (рис. 3г).

Теорема 1. Плоскость, параллельная плоскости основания цилиндра, пересекает его боковую поверхность по окружности, равной окружности основания.

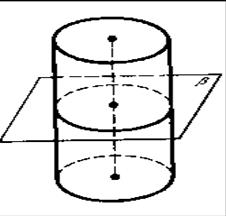Доказательство. Пусть β − плоскость, параллельная плоскости основания цилиндра. Параллельный перенос в направлении оси цилиндра, совмещающий плоскость β с плоскостью основания цилиндра, совмещает сечение боковой поверхности плоскостью β с окружностью основания. Теорема доказана.

1.4. Площадь цилиндра

Площадь боковой поверхности цилиндра.

За площадь боковой поверхности цилиндра принимается предел, к которому стремится площадь боковой поверхности правильной призмы, вписанной в цилиндр, когда число сторон основания этой призмы неограниченно возрастет.

Теорема 2. Площадь боковой поверхности цилиндра равна произведению длины окружности его основания на высоту (S_бок.ц = 2πRH, где R − радиус основания цилиндра, Н − высота цилиндра).

а) 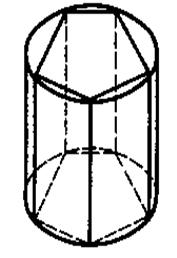б)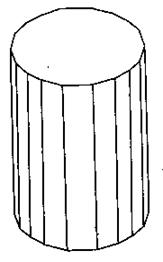
Рис. 4 − Площадь боковой поверхности цилиндра

Доказательство.

Пусть P_n и Н соответственно периметр основания и высота правильной n-угольной призмы, вписанной в цилиндр (рис. 4, а). Тогда площадь боковой поверхности этой призмы S_бок.ц − P_n H. Предположим, что число сторон многоугольника, вписанного в основание, неограниченно растет (рис. 4, б). Тогда периметр P_n стремится к длине окружности С = 2πR, где R— радиус основания цилиндра, а высота H не изменяется. Таким образом, площадь боковой поверхности призмы стремится к пределу 2πRH, т. е. площадь боковой поверхности цилиндра равна S_бок.ц = 2πRH. Теорема доказана.

Площадь полной поверхности цилиндра.

Площадью полной поверхности цилиндра называется сумма площадей боковой поверхности и двух оснований. Площадь каждого основания цилиндра равна πR² , следовательно, площадь полной поверхности цилиндра S_полн вычисляется по формуле S_бок.ц = 2πRH+ 2πR² .

r

T1

T

F

F1

F

T

?)

F

?)

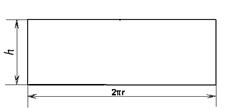
Рис. 5 − Площадь полной поверхности цилиндра

Если боковую поверхность цилиндра разрезать по образующей FT (рис. 5, а) и развернуть так, чтобы все образующие оказались в одной плоскости, то в результате мы получим прямоугольник FTT1F1, который называется разверткой боковой поверхности цилиндра. Сторона FF1 прямоугольника есть развертка окружности основания цилиндра, следовательно, FF1=2πR, а его сторона FT равна образующей цилиндра, т. е. FT = Н (рис. 5, б). Таким образом, площадь FT∙FF1=2πRH развертки цилиндра равна пло­щади его боковой поверхности.

1.5. Объем цилиндра

Если геометрическое тело простое, то есть допускает разбиение на конечное число треугольных пирамид, то его объем равен сумме объемов этих пирамид. Для произвольного тела объем определяется следующим образом.

Данное тело имеет объем V, если существует содержащие его простые тела и содержащиеся в нем простые тела с объемами, сколько угодно мало отличающимися от V.

Применим это определение к нахождению объема цилиндра с радиусом основания R и высотой Н.

При выводе формулы для площади круга были построены такие два n-угольника (один − содержащий круг, другой − содержащийся в круге), что их площади при неограниченном увеличении n неограниченно приближались к площади круга. Построим такие многоугольники для круга в основании цилиндра. Пусть Р − многоугольник, содержащий круг, а Р' − многоугольник, содержащийся в круге (рис. 6).

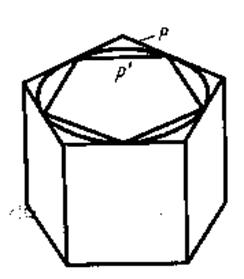
Рис. 7 − Цилиндр с описанной и вписанной в него призмой

Построим две прямые призмы с основаниями Р и Р' и высотой Н, равной высоте цилиндра. Первая призма содержит цилиндр, а вторая призма содержится в цилиндре. Так как при неограниченном увеличении n площади оснований призм неограниченно приближаются к площади основания цилиндра S, то их объемы неограниченно приближаются к SН. Согласно определению объем цилиндра

V = SH = πR² H.

Итак, объем цилиндра равен произведению площади основания на высоту.

2 Практическая часть (задачи)

Задача 1.

Осевое сечение цилиндра − квадрат, площадь которого Q.