Учебное пособие: Цилиндр

Дано: цилиндр, квадрат − осевое сечение цилиндра, S_{квадрата} = Q.

Найти: S_{осн.цил.}

Решение:

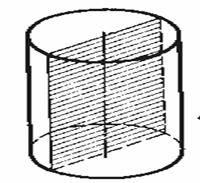
Сторона квадрата равна . Она равна диаметру основания. Поэтому площадь основания равна .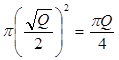

Ответ: S_{осн.цил.} =

Задача 2.

В цилиндр вписана правильная шестиугольная призма. Найдите угол между диагональю ее боковой грани и осью цилиндра, если радиус основания равен высоте цилиндра.

Дано: цилиндр, правильная шестиугольная призма вписанная в цилиндр, радиус основания = высоте цилиндра.

Найти: угол между диагональю ее боковой грани и осью цилиндра.

Решение: Боковые грани призмы − квадраты, так как сторона правильного шестиугольника, вписанного в окружность, равна радиусу.

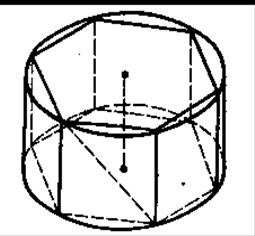
Ребра призмы параллельны оси цилиндра, поэтому угол между диагональю грани и осью цилиндра равен углу между диагональю и боковым ребром. А это угол равен 45°, так как грани − квадраты.

Ответ: угол между диагональю ее боковой грани и осью цилиндра = 45°.

Задача 3.

Высота цилиндра 6см, радиус основания 5см.

Найдите площадь сечения, проведенного параллельно оси цилиндра на расстоянии 4см от нее.

Дано: Н = 6см, R = 5см, ОЕ = 4см.

Найти: S_сеч.

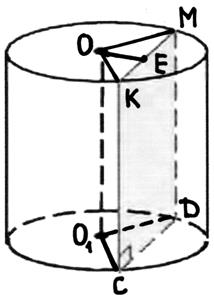
Решение:

S_сеч. = КМ×КС,

ОЕ = 4 см, КС = 6 см.

Треугольник ОКМ − равнобедренный (ОК = ОМ = R = 5 см),

треугольник ОЕК − прямоугольный.

Из треугольника ОЕК, по теореме Пифагора:

ЕК = ,

КМ = 2ЕК = 2×3 = 6,

S_сеч. = 6×6 = 36 см² .

Ответ: S_сеч. = 36 см² .

Задача 4.

Высота цилиндра 12см, радиус основания 10см.