Учебное пособие: Цилиндр

Из прямоугольного ∆ АВD по теореме Пифагора: ВD² − 2AB² , откуда сторона квадрата АВ 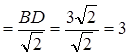(см). Поэтому высота цилиндра АВ = 3 см, радиус цилиндра ОА − 1,5 см.

Площадь боковой поверхности S_бок.ц = 2πRH = 2π×1,5×3 = 9π (см² ).

Площадь основания S_осн. = 2πR² = 2π×1,5² = 4,5π (см² ).

Площадь полной поверхности S_{пов.цил.} = S_бок.ц + S_осн. = 9π + 4,5π = 13,5 π (см² ).

Ответ: 13,5 π (см² ).

Задача 8.

В цилиндр вписана правильная шестиугольная призма.

Найдите отношения объема призмы к объему цилиндра.

Дано: цилиндр, правильная шестиугольная призма вписана в цилиндр, а − сторона призмы.

Найти: .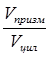

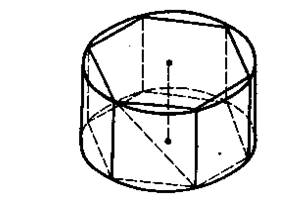
а

а

Решение:

=

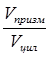а₆ = R

Ответ: = .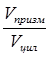

Задача 9.

Диаметр основания цилиндра 1м.

Найдите площадь боковой поверхности цилиндра.

Дано: цилиндр, d = АВ = 1м.

Найти: S_бок.ц.

d

Решение:

S_бок. = 2πRh,

R = = 0,5 м,

S_бок. = 2πR × 2πR = (2πR)² = 4π² ×0,25 = π²

Ответ: S_бок. = π² (м² ).

Задача 10.

Найдите радиус основания цилиндра наибольшего объема, вписанного в конус, радиус основания которого равен 3.

Дано: конус, цилиндр – вписан в конус, ОВ – радиус конуса, ОВ = 3.

Найти: r − радиус основания цилиндра.

Решение: