Найдите расстояние от этого сечения до оси.
Дано: СК = h = 12см, R = ОК = ОМ = 10см.
Найти: ОЕ.
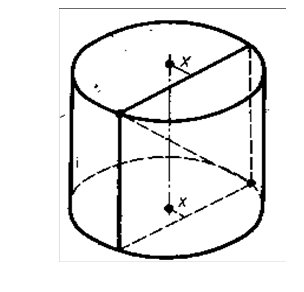
Решение:
СК равна высоте, то есть СК = 12 см. Так как в сечении получился квадрат, то КМ = СК = 12см.
ОК − радиус основания, ОК = 10см.
Треугольник ОКЕ – прямоугольный, где ОК = 10см, КЕ = 6см.
По теореме Пифагора:
ОЕ = 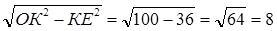
Ответ: ОЕ = 8см.
Задача 5.
В цилиндр наклонно вписан квадрат так, что все его вершины лежат на окружностях основания. Найдите сторону квадрата, если высота цилиндра равна 2см, а радиус основания равен 7см.
Дано: цилиндр, h = 2см, R – 7см, АВСD − наклонно вписанный квадрат.
?????: ??.




Решение:
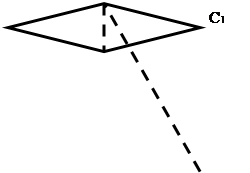
Достроим квадрат АВСD до прямого прямоугольного параллелограмма АВС1 D1 А1 В1 СD с диагональным сечением АВСD.
Угол АВС1 = 90°. Так как вписанный в окружность угол, стороны которого проходят через две данные точки окружности, равен половине угла между радиусами, проходившими в эти точки, или дополняет половину этого угла до 180°, то АС1 есть диаметр окружности верхнего основания цилиндра.
Рассмотрим прямоугольный треугольник СС1 А1 − катет СС1 , есть образующая цилиндра и СС1 = 2АС, катет АС1 есть диаметр цилиндра и АС1 = 14. По теореме Пифагора АС = 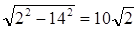 (см).
(см).
Из прямоугольного равнобедренного треугольника АВС по теореме Пифагора сторона квадрата АВ = 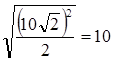 см.
см.
Ответ: АВ = 10 см.
Задача 6.
Объем цилиндра 120 см2 , его высота 3,6 см.
Найти радиус цилиндра.
Дано: V = 120 см2 , h = 3,6 см.
Найти: r
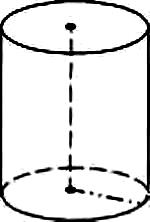
Решение:
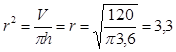
Ответ: r = 3,3.
Задача 7.
Осевым сечением цилиндра является квадрат, диагональ которого равна 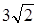 см.
см.
Найдите площадь поверхности цилиндра.
Дано: цилиндр, АВСD − осевое сечение, АВ = АD, ВD = 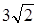 см.
см.
Найти: Sпов.цил.

К-во Просмотров: 721
Бесплатно скачать Учебное пособие: Цилиндр


![]()



![]() (см).
(см).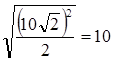 см.
см.
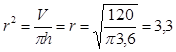
![]() см.
см.![]() см.
см.
