Учебное пособие: Выборочный метод
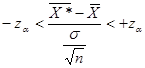(1.9.22)
которое эквивалентно неравенству:
(1.9.23)
Величина 
называется предельной ошибкой выборки.
Таким образом, мы имеем доверительный интервал для генеральной средней:
(
; 
)
Наоборот, если задана предельная ошибка ε , а требуется определить вероятность Р, то схема решения задачи следующая:
ε→z=
→Ф(z )→P =2Ф(z ) (1.9.24)
Наконец, определение объема выборки п по данным Р и ε производится по следующей схеме:
P =2Ф(z ) →z →n =
(1.9.25)
Пример 1.9.4. Взвешивание 50 случайно отобранных коробок печенья дало 
=1200г. Определить с вероятностью Р = 0,95 доверительные границы для среднего веса коробки печенья 
в генеральной совокупности, если есть основания полагать, что генеральная дисперсия σ2 = 11664.
Решение:
Дано: n =50; = 1200; σ2 =11664 (
= 108); Р = 0,95.
Из равенства Р = 2Ф(z )=0,95 по таблице значений интегральной функции Лапласа находим z=1,96, откуда:
ε=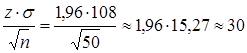
(г)
Таким образом, получаем доверительный интервал:
1200 — 30 < < 1200 + 30.
Пример 1.9.5 Определить, с какой доверительной вероятностью можно утверждать, что при данном объеме выборки (50 коробок) ошибка выборки не превысит 20 г.
Решение:
По величине ε=20 вычисляем 
, откуда по таблице Ф(z ): Р = 2Ф(1,31)≈0,81
Пример 1.9.6. Определить необходимый объем выборки n , который с вероятностью 0,99 гарантировал бы ошибку выборки не более чем ε = 20г.
Решение:
Из Р = 2Ф(z ) =0,99 находим z = 2,58, откуда:
коробок
Предположение о том, что генеральная дисперсия σ2 известна при неизвестной генеральной средней, на практике выполняется весьма редко. Чаще всего мы имеем лишь выборочные данные и можем дать лишь выборочную оценку s 2 неизвестной дисперсии σ2 .
Статистика
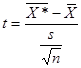(1.9.26)
подчиняется закону распределения Стьюдента с v = n —1 степенями свободы. Однако при больших значениях параметра v (v ≥ 30) распределение Стьюдента практически совпадает с нормальным. Поэтому в случае больших выборок схема решения задач остается прежней, даже если вместо 'Неизве стного генерального среднего квадратического отклонения а используется его выборочная оценка s .
3.5.2. Малая выборка