Дипломная работа: Дифференциальная геометрия торсов в пространстве 1R4 с псевдоевклидовой касательной плоскостью

Определение 1.3. Ортогональным дополнением к векторному пространству LÌ1R4 называется векторное пространство, образованное всеми векторами, ортогональными к пространству L.

Пример. Найдем множество векторов, ортогональных к вектору . Если вектор ортогонален , то . Отсюда,

=.

Таким образом, ортогональным дополнением к вектору является множество векторов . Эти векторы определяют 3-плоскость которое является 3-плоскостью вида 1R3. Следовательно, R1^1R3. Это означает, что к прямой R1 ортогональной является 3-плоскость типа1R3. Верно и обратное.

Аналогично найдем множество векторов ортогональных к вектору. Если вектор ортогонален , то . Отсюда,

=.

Множество векторов, ортогональных вектору , имеет вид и определяет 3-плоскость которое является 3-плосткостью вида R3. Следовательно, 1R1^R3. Это означает, что к прямой 1R3 ортогональной является 3-плоскость типа R3. Верно и обратное.

Рассмотрим вектор () и найдем множество векторов ортогональных к данному вектору. Если вектор ортогонален (), то .

Получаем, что

=.

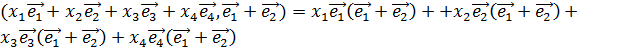Отсюда, , а — произвольные. - это множество векторов, ортогональных вектору () и определяет 3-плоскость которое является 3-плосткостью вида . Значит, ^. Это означает, что к прямой ортогональной является 3-плоскость типа . Верно и обратное.

Заметим, что Ì.

Найдем множество векторов, ортогональных к векторам . Если вектор ортогонален , то Отсюда,

Û

Таким образом, ортогональным дополнением к векторам является множество векторов . Эти векторы определяют 2-плоскость которая является 2-плосткостью вида 1R2. Следовательно, R2 ^1R2 (к двумерной плоскости R2 ортогональной является плоскость вида 1R2).

Найдем множество векторов, ортогональных к векторам . Если вектор ортогонален , то Отсюда,

Û

Таким образом, ортогональным дополнением к векторам является множество векторов . Эти векторы определяют 2-плоскость которое является 2-плосткостью вида R2, Следовательно, R2 ^1R2 (к двумерной плоскости R2 ортогональной является плоскость вида 1R2 ). Верно и обратное.

Найдем множество векторов, ортогональных к векторамЕсли вектор ортогонален , то

Отсюда,

Û

Û

Таким образом, ортогональным дополнением к векторам является множество векторов . Эти векторы определяют 2-плоскость которая является 2-плосткостью вида . Следовательно, ^.

Таким образом, получена теорема.

Теорема 1.1. В пространстве 1R4 существуют следующие типы прямых, плоскостей и 3-плоскостей:

- прямые: R1, 1R1,.

- 2-плоскости: R2, 1R2,.

- 3-плоскости: R3, 1R3,.