Дипломная работа: Дифференциальная геометрия торсов в пространстве 1R4 с псевдоевклидовой касательной плоскостью
![]()
![]() r(u),
r(u), ![]() ;
;
действительно, вектор NM коллинеарен единичному вектору ![]() и потому отличается от него лишь скалярным множителем, равным длине NM с соответствующим знаком, т. е. множителем v .
и потому отличается от него лишь скалярным множителем, равным длине NM с соответствующим знаком, т. е. множителем v .
Итак, окончательно ![]() .
.
В результате радиус-вектор произвольной точки М на произвольной образующей выразился как функция двух независимых параметров u , v . Мы получили, таким образом, параметрическое представление линейчатой поверхности, именно той, которая образована прямыми (образующими) построенного нами однопараметрического семейства прямых.
Фиксируя в этом уравнении u и меняя v , мы движемся, очевидно, по образующей, отвечающей данному значению u . Следовательно, семейством координатных линий v у нас будут служить образующие. Если же фиксировать v и менять u , то мы идем по образующим «параллельно» направляющей линии в том смысле, что расстояние NM = v остается постоянным.
Таким образом, координатные линии u образуют семейство линий, «параллельных» направляющей линии, которая сама также входит в это семейство и отвечает случаю, когда v фиксировано на значении 0.
Заметим, что направляющая линия геометрически ничем на заданной линейчатой поверхности не выделяется. В качестве направляющей может быть взята любая кривая на линейчатой поверхности, последовательно пересекающаяся с ее образующими; произвол этот отразится только на выборе параметров u , v на поверхности.
Вычислим теперь частные производные радиус-вектора по параметрам. Очевидно,
![]() (16)
(16)
Составим векторное произведение этих векторов, направленное, как мы знаем, по нормали к поверхности:
![]() (17)
(17)
Исследуем поведение нормали к линейчатой поверхности, когда точка движется по поверхности вдоль какой-нибудь образующей, т. е. когда мы меняем v при фиксированном u . Так как ![]() , l являются функциями только u , то векторные произведения
, l являются функциями только u , то векторные произведения ![]() и
и ![]() остаются постоянными, и правая часть (17) может меняться лишь вследствие изменения коэффициента v .
остаются постоянными, и правая часть (17) может меняться лишь вследствие изменения коэффициента v .
Здесь мы будем различать два случая, общий и специальный.
Общий случай: векторные произведения ![]() и
и ![]() не коллинеарны. В этом случае при движении вдоль образующей, т. е. при изменении v , первое слагаемое в правой части (17) постоянно, второе же, ему не параллельное, изменяется пропорционально v . В результате вся правая часть представляет собой вектор, направление которого меняется вместе с v .
не коллинеарны. В этом случае при движении вдоль образующей, т. е. при изменении v , первое слагаемое в правой части (17) постоянно, второе же, ему не параллельное, изменяется пропорционально v . В результате вся правая часть представляет собой вектор, направление которого меняется вместе с v .
|
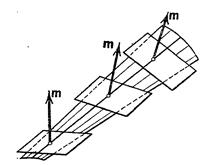
Следовательно, вдоль образующей направление нормали к поверхности меняется от точки к точке. Очевидно, что касательная плоскость в какой-нибудь точке на данной образующей проходит через эту образующую (так как образующая является своей собственной касательной). Поэтому при движении точки касания вдоль образующей касательная плоскость, все время проходя через образующую, вращается около нее. В этом случае линейчатая поверхность называется косой (Рис. 3.2).
Специальный случай: векторные произведения ![]() и
и ![]() коллинеарны.
коллинеарны.
|
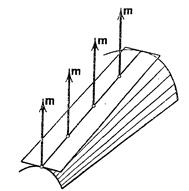
В этом случае оба слагаемых в правой части (17) параллельны друг другу (а следовательно, и своей сумме) при любом значении v . Таким образом, все нормали вдоль данной образующей параллельны между собой, так как они параллельны векторам ![]() и
и ![]() . Когда точка касания движется вдоль образующей, то касательная плоскость проходит все время через образующую; и так как касательная плоскость должна, кроме того, оставаться перпендикулярной к неизменному направлению нормали, то она не может вращаться около образующей и остается неподвижной.
. Когда точка касания движется вдоль образующей, то касательная плоскость проходит все время через образующую; и так как касательная плоскость должна, кроме того, оставаться перпендикулярной к неизменному направлению нормали, то она не может вращаться около образующей и остается неподвижной.
Итак, в рассматриваемом случае касательные плоскости к поверхности в точках, расположенных на одной и той же образующей, совпадают между собой. Такую линейчатую поверхность мы будем называть развертывающейся поверхностью (Рис. 3.3).
Обратно, если мы имеем развертывающуюся поверхность, т. е. касательная плоскость для всех точек образующей одна и та же, и нормали вдоль образующей параллельны, то направление вектора (17) не зависит от значения v , что возможно лишь в случае
![]() ||
|| ![]() (18)
(18)
Таким образом, условие (18) необходимо и достаточно для того, чтобы линейчатая поверхность оказалась развертывающейся. Этому условию можно придать более простую форму.
Общее направление двух векторных произведений будет ортогональным ко всем их множителям, т. е. к векторам ![]() ,
, ![]() , которые, таким образом, оказываются компланарными (параллельными одной плоскости).
, которые, таким образом, оказываются компланарными (параллельными одной плоскости).
Легко видеть, что это условие и достаточно. Итак, условие (18) может быть переписано в эквивалентном виде ![]() ,
, ![]() компланарны, т.е.
компланарны, т.е.
(![]() ,
, ![]() = 0. (19).
= 0. (19).
Это условие наложено, как мы видим, на вектор-функции ![]() (радиус-вектор направляющей кривой) и
(радиус-вектор направляющей кривой) и ![]() , (единичный вектор на образующей). Плоскость векторов (19) будет параллельна векторам (16) при любом значении v , т. е. параллельна касательной плоскости, проходящей через соответствующую образующую.
, (единичный вектор на образующей). Плоскость векторов (19) будет параллельна векторам (16) при любом значении v , т. е. параллельна касательной плоскости, проходящей через соответствующую образующую.
§4. Торсы в пространстве 1R4