Дипломная работа: Дослідження нестандартних методів рішення рівнянь і нерівностей.
Позначивши кількість чоловіків за х, кількість жінок за у, ми прийдемо до рівняння
Зх + 2y+
( х-y)= 100
Загального рішення лінійних дофантових рівнянь у ті часи ще не знали й задовольнялися лише декількома рішеннями, що задовольняють умові задачі. У самого Алькуина було наведено лише одне рішення цієї задачі: чоловіків, жінок і дітей було 11, 15 і 74, а задача має 784 рішення в натуральних числах.
Задачі, що приводять до лінійних дофантових рівнянням, були в Леонардо Пизанського (Фибоначчи) (1180 - 1240), в «Арифметиці» Л. Ф. Магницького.
Відоме рівняння Піфагора (VI в. до н.е.) х2 + в2 = z2 вирішують у натуральних числах. Його рішеннями служать трійки чисел (х; в; z):
x = (m2 -n2 )l, y = 2mnl, z = (m2 + n2 )l,
де т, п, l - будь-які натуральні числа (т> п). Ці формули допомагають знаходити прямокутні трикутники, довжини сторін яких є натуральними числами.
В 1630 р. французький математик Пьер Ферма (1601 — 1665) сформулював гіпотезу, що називають великою (або великий) теоремою Ферма: «Рівняння хп + уп = zn для натурального п ≥ 3 не має рішень у натуральних числах». Ферма не довів свою теорему в загальному випадку, але відома його запис на полях «Арифметики» Диофанта: «...неможливо куб записати у вигляді суми двох кубів, або парний ступінь у вигляді суми таких же ступенів, або взагалі будь-яке число, що є ступенем більшої, ніж друга, не можна записати у вигляді суми двох таких же ступенів. У мене є воістину дивний доказ цього твердження, але поля ці занадто вузькі, щоб його вмістити». Пізніше в паперах Ферма було знайдене доказ його теореми для п= 4. З тих пор більше 300 років математики намагалися довести велику теорему Ферма. В 1770 р. Л.Ейлер довів теорему Ферма для п = 3, в 1825 р. Адриен Лежандр (1752 1833) і Петер Дирихле (1805 - 1859) - для п = 5. Доказ великої теореми Ферма в загальному випадку не вдавався довгі роки. І тільки в 1995 р. Ендрю Вайлс довів цю теорему.
2. РІШЕННЯ ЗАДАЧ ІЗ ВИКОРИСТАННЯМ ВЛАСТИВОСТЕЙ ФУНКЦІЇ
Не всяке рівняння f(x) = g(x) або нерівність у результаті перетворень або за допомогою вдалої заміни змінної може бути зведене до рівняння або нерівності того або іншого стандартного виду, для якого існує певний алгоритм рішення. У таких випадках іноді виявляється корисним використовувати деякі властивості функцій, такі як монотонність, періодичність, обмеженість, парність і ін.
2.1 Використання монотонності функції
Функція f (x) називається зростаючої на проміжку D, якщо для будь-яких чисел x1 і x2 із проміжку D таких, що x1 < x2 , виконується нерівність f (x1 ) < f (x2 ).
Функція f (x) називається убутної на проміжку D, якщо для будь-яких чисел x1 і x2 із проміжку D таких, що x1 < x2 , виконується нерівність f (x1 ) > f (x2 ).
На показаному на малюнку 1 графіку
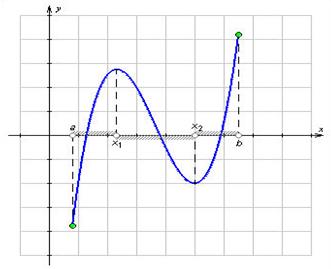
Малюнок 1
Функція y = f (x), 
, зростає на кожному із проміжків [a; x1 ) і (x2 ; b] і убуває на проміжку (x1 ; x2 ). Зверніть увагу, що функція зростає на кожному із проміжків [a; x1 ) і (x2 ; b], але не на об'єднанні проміжків 
Якщо функція зростає або убуває на деякому проміжку, то вона називається монотонної на цьому проміжку.
Помітимо, що якщо f – монотонна функція на проміжку D (f (x)), те рівняння f (x) = const не може мати більше одного кореня на цьому проміжку.
Дійсно, якщо x1 < x2 – корінь цього рівняння на проміжку D (f(x)), те f (x1 ) = f (x2 ) = 0, що суперечить умові монотонності.
Перелічимо властивості монотонних функцій (передбачається, що всі функції визначені на деякому проміжку D).
Сума декількох зростаючих функцій є зростаючою функцією.
Добуток ненегативних зростаючих функцій є зростаюча функція.
Якщо функція f зростає, то функції cf (c > 0) і f + c також зростають, а функція cf (c < 0) убуває. Тут c - деяка константа.
Якщо функція f зростає й зберігає знак, то функція 
убуває.
Якщо функція f зростає й ненегативна, то fn де n
N, також зростає.
Якщо функція f зростає й n – непарне число, то fn також зростає.
Композиція g (f (x)) зростаючих функцій f і g також зростає.
Аналогічні твердження можна сформулювати й для убутної функції.