Дипломная работа: Дослідження нестандартних методів рішення рівнянь і нерівностей.

має період .

Тоді функція має період

Відповідь: ?.

Приклад 2.4.3 Нехай - періодична функція з періодом 3 така, що

; .

Вирішите рівняння:

(7)

Графік функції на множині [0;3) зображений на малюнку 3:

x

y

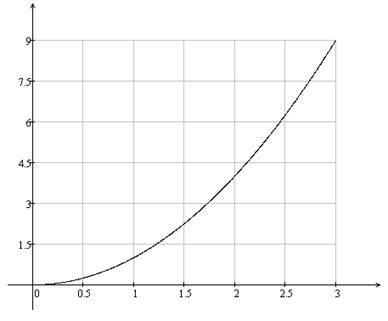
Малюнок 5

Таким чином 3 - період функції , те, тоді рівняння (7) прикмет вид , розглянемо два випадки.

1) нехай , тобто , тоді рівняння прийме вид:

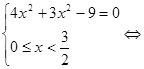
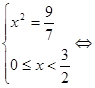
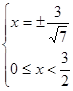, значить і виходить,

2) нехай те, тоді рівняння прийме вид:

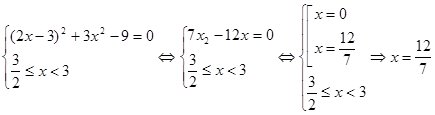; отже ,

таким чином , .

Відповідь: .

2.4 Використання парності функції

Функція f (x) називається парної, якщо для кожного виконуються рівності:

1) ,

2) f (–x) = f (x).

Графік парної функції на всій області визначення симетричний щодо осі OY. Прикладами парних функцій можуть служити y = cos x, y = |x|, y = x² + |x|

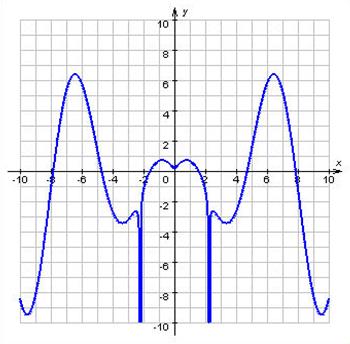
Графік парної функції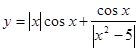

Функція f (x) називається непарної, якщо для кожного виконуються рівності:

1) ,

2) f (–x) = –f (x).

Іншими словами функція називається непарної, якщо її графік на всій області визначення симетричні відносно початку координат. Прикладами непарних функцій є y = sin x, y = x³ .