Дипломная работа: Интеграл Лебега-Стилтьеса

Во второй главе рассмотрены основные понятия, определение самого интеграла, свойства, способы вычисления, рассмотрено множество примеров.

Третья глава посвящена применению интеграла Стилтьеса в других разделах математики и в других науках.

Глава I. Развитие понятия интеграла

1.1 Проблема моментов

Введение понятия интеграла Стилтьеса и последующая его разработка связаны с проблемой моментов, состоящей в следующем. Пусть задана последовательность чисел ; требуется найти такую функцию распределения , чтобы члены заданной последовательности были моментами, т.е. 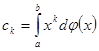. Если a и b конечны, то поставленная задача называется проблемой моментов в конечном интервале; если , то получаем проблему моментов Стилтьеса.

Проблема моментов первоначально ставилась в менее общей форме. А именно по заданной последовательности чисел ищется такая функция , чтобы имели место равенства 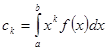. Целесообразность привлечения интеграла Стилтьеса для постановки и решения проблемы моментов напрашивается довольно естественно. С таким положением вещей и столкнулся Стилтьес при изучении непрерывных дробей, и именно в результате этих исследований он предложил своё обобщение интеграла.

Ранние исследования Стилтьеса изложены в его статье о механических квадратурах, в которой выясняется, позволяют ли формулы квадратур получать неограниченное приближение интеграла в смысле Римана. Во вводной части статьи Стилтьес решает задачу об определении многочлена

Условиями

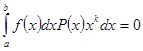
(1)

при неотрицательной на .

Мы коснемся двух моментов из содержания его статьи.

Первый относится к задаче о степени приближения, даваемого квадратурной формулой Гаусса:

Здесь Стилтьес пользуется доказанными им формулами П.Л. Чебышева в виде

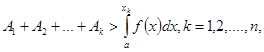
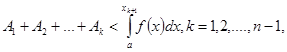
где . (2)

Он показывает, что если в квадратурной формуле Гаусса в качестве брать числа , получаемые по формуле (2) из цепной дроби, соответствующей интегралу , а будут корнями знаменателей подходящих дробей, то формула Гаусса даст сколь угодно точное приближение при возрастании . Для этой цепной дроби числа , очевидно, удовлетворяют неравенствам

(3)

так как в этом случае .

Вторым моментом является следующий. Отметив, что его результаты полезны при изучении вопроса о квадратуре интеграла 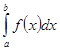, Стилтьес ставит вопрос о квадратурных формулах для интеграла вида

. (4)

Он ограничивается тем частным случаем, когда - произвольная интегрируемая по Риману функция, а такова, что внутри не существует интервала , в котором , и показывает, что в этом случае аппроксимация возможна со сколь угодно большой степенью точности. Доказательство этого факта опирается на то, что функция

(5)

является непрерывной и строго монотонной, а потому существует обратная функция , и в интеграле (4) возможна замена переменных

сводящих интеграл (4) к уже изученному Стилтьесом случаю.

По поводу же общего случая Стилтьес указал, что "условия, налагаемые на функции , делаются источником трудностей, которых удастся избежать лишь с помощью новых исследований о самих принципах интегрального исчисления". Действительно, если не удовлетворяет условию отсутствия в интервала , в котором , то она может оказаться не монотонной, поэтому обращение в том виде, в каком такую замену тогда производили, становится невозможным, и квадратуру интеграла (4) уже нельзя свести к квадратуре интеграла .

Приведенные слова Стилтьеса показывают, что уже в 1884 г. он был в некоторой степени подготовлен к пересмотру понятия интеграла. К мысли о таком пересмотре его приводил прием замены переменных, который играл заметную роль в последующей истории интеграла Стилтьеса.