Дипломная работа: Интеграл Лебега-Стилтьеса

откуда и следует выполнение условия (4), а стало быть и существование интеграла.

В общем случае, если функция имеет ограниченное изменение, она представима в виде разности двух ограниченных возрастающих функций: . В соответствии с этим преобразуется и сумма Стилтьеса, отвечающая функции :

.

Так как по уже доказанному каждая из сумм и при стремится к конечному пределу, то это справедливо и относительно суммы , что и требовалось доказать.

Можно ослабить условия, налагаемые на функцию , если одновременно усилить требования к функции :

Если функция интегрируема в в смысле Римана, а удовлетворяет условию Липшица:

(6)

то интеграл (5) существует.

Для того чтобы опять иметь возможность применить установленный выше критерий, предположим сначала функцию не только удовлетворяющей условию (6), но и монотонно возрастающей.

Ввиду (6), очевидно, , так что

.

Но последняя сумма при и сама стремится к 0 вследствие интегрируемости (в смысле Римана) функции , а тогда стремится к нулю и первая сумма, что доказывает существование интеграла (5).

В общем случае функции , удовлетворяющей условию Липшица (6), представим в виде разности

Функция , очевидно, удовлетворяет условию Липшица и в то же время монотонно возрастает. То же справедливо и для функции , так как, в силу (6), при

и

В таком случае рассуждение завершается, как и выше.

III. Если функция интегрируема в смысле Римана, а функция представима в виде интеграла с переменным верхним пределом:

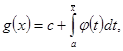(7)

где абсолютно интегрируема, в промежутке , то интеграл (5) существует.

Пусть , так что монотонно возрастает. Если интегрируема в собственном смысле и, следовательно, ограничена: то для

Имеем

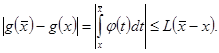
Таким образом, в этом случае удовлетворяет условию Липшица, и интеграл существует в силу 2.

Предположим теперь, что интегрируема в несобственном смысле. Ограничимся случаем одной особой точки, скажем . Прежде всего, по произвольно взятому выберем так, чтобы было

(8)