Дипломная работа: Интеграл Лебега-Стилтьеса

Разобьем промежуток по произволу на части и составим сумму

Она разлагается на две суммы , из коих первая отвечает промежуткам, целиком содержащимся в промежутке , а вторая - остальным промежуткам. Последние наверное содержаться в промежутке , если только ; тогда, в силу (8),

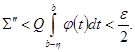
С другой стороны, так как в промежутке функция интегрируема в собственном смысле, то по доказанному при достаточно малом и сумма станет меньше . Отсюда следует (4), что и требовалось доказать.

В общем случае, когда функция абсолютно интегрируема в промежутке , мы рассмотрим функции

очевидно, неотрицательные и интегрируемые в названном промежутке. Так как

то вопрос сводится, как и выше, к уже рассмотренному случаю.

Замечание. Пусть функция непрерывна в промежутке и имеет, исключая разве лишь конечное число точек, производную , причем эта производная интегрируема (в собственном или несобственном смысле) от до ; тогда, как известно, имеет место формула типа (7):

.

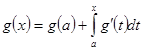Если абсолютно интегрируема, то к функции полностью приложимо изложенное в 3.

2.4 Свойства интеграла Стилтьеса

Из определения интеграла Стилтьеса непосредственно вытекают следующие его свойства:

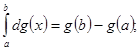
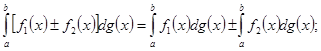
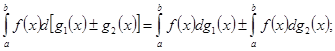
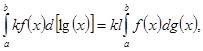
При этом в случаях из существования интегралов в правой части вытекает существование интеграла в левой части.

Затем имеем

в предположении, что и существуют все три интеграла.

Для доказательства этой формулы достаточно лишь озаботиться включением точки в число точек деления промежутка при составлении суммы Стилтьеса для интеграла .

По поводу этой формулы сделаем ряд замечаний. Прежде всего, из существования интеграла следует уже существование обоих интегралов

и .

Для своеобразного предельного процесса, с помощью которого из стилтьесовской суммы получается интеграл Стилтьеса, имеет место принцип сходимости Больцано-Коши. Таким образом, по заданному ввиду существования интеграла найдется такое , что любые две суммы и Стилтьеса, которым отвечают и , разнятся меньше чем на . Если при этом в состав точек деления включить точку , а точки деления, приходящиеся на промежуток , брать в обоих случаях одними и теми же, то разность сведется к разности двух сумм Стилтьеса, относящихся уже к промежутку , ибо прочие слагаемые взаимно уничтожатся. Применяя к промежутку и вычисленным для него стилтьесовским суммам тот же принцип сходимости, заключим о существовании интеграла . Аналогично устанавливается и существование интеграла .

Особенно заслуживает быть отмеченным тот не имеющий прецедентов факт, что из существования обоих интегралов и , вообще говоря, не вытекает существование интеграла .

Чтобы убедиться в этом, достаточно рассмотреть пример. Пусть в промежутке функции и заданы следующими равенствами:

;