Дипломная работа: Интеграл Лебега-Стилтьеса

Эти формулы позволяют по цепной дроби (6) найти её разложение в ряд (9). Обратная же задача - по разложению (9) найти дробь (6) - неизбежно приводит к решению более или менее общей проблемы моментов.

В самом деле, Стилтьесу была известна чебышевско-марковская интерпретация , как массы, сосредоточенной в точке , являющейся корнем . Естественно было распространить эту интерпретацию и на предельный случай, рассматривая как массы, расположенные в нулях функции (или ). После введения формул (10) Стилтьес пишет: "Рассмотрим на бесконечной прямой распределение массы (положительной), при котором на расстоянии от начала сосредоточена масса .

Сумма

может быть названа моментом порядка масс относительно начала. В таком случае из предшествующих формул следует, что момент порядка системы масс

имеет значение .

Равным образом система масс , где , будем иметь те же моменты .

Мы назовем проблемой моментов следующую задачу:

Найти распределение положительной массы на прямой , если даны моменты порядка ".

Действительно, формулы (10) приводят к постановке проблемы моментов, если принято истолкование и как масс, а как соответствующих расстояний этих масс от начала координат.

Цепные дроби рассматривающегося П.Л. Чебышевым и А.А. Марковым типа получились из разложения интеграла (7) и все корни знаменателей их подходящих дробей были заключены в промежутке . Стилтьес же не связывал рассматриваемые им дроби с заранее данным аналитическим выражением в виде интеграла, и корни , оказывались в общем случае распределенными по всей положительной части числовой оси. Поэтому закономерным был выход в проблеме моментов за пределы конечного интервала и рассмотрение её на интервале . Далее, поскольку рассматриваются как моменты массы относительно начала координат, то прежнее определение момента через интеграл Римана 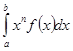становилось недостаточным, существенно ограничивая класс последовательностей чисел ; даже для таких распределений массы, как концентрация её в отдельных точках, приходилось принимать довольно неожиданные предположения относительно функции плотности , как это было у русских ученых. Между тем, как показал Стилтьес, на последовательность чисел достаточно было наложить довольно слабые ограничения, чтобы ряд (9) можно было обратить в цепную дробь (6), а тем самым найти функции . Зная же эти функции, мы тем самым знаем решение системы уравнений (10), т.е. решение проблемы моментов. Если при этом и , и попарно совпадут, то получится определенное решение: если же они попарно различны, то решений по крайней мере два: системы и . Следовательно, общность цепных дробей вида (6) достаточно широка, чтобы сделать вывод о разрешимости проблемы моментов для интервала , но для этого требовалось дать иное определение моментов.

Физическое определение момента материальной точки в соединении с обычным для физиков и математиков переходом от момента точки к моменту отрезка приводило к новому определению интеграла, тесно связанному с функциями распределения.

Таким образом, именно для того, чтобы описать в форме некоторого аналитического выражения физическое понятие момента, Стилтьес ввел новое понятие интеграла, причем последнее, как это обычно и случается в математике, оказалось имеющим более общий характер, чем исходное физическое понятие.

Он рассмотрел интеграл 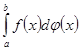для случая произвольной непрерывной и произвольной возрастающей . В этих предположениях он высказал без доказательства теорему существования интеграла, отметив лишь, что оно может быть осуществлено так же, как и для определенного интеграла Римана. Затем в этих же общих приложениях он доказал одну из важнейших формул теории нового интеграла, а именно формулу интегрирования по частям. И теорему существования, и формулу интегрирования по частям мы рассмотрим в последующих главах.

Глава II. Интеграл Стилтьеса

2.1 Определение интеграла Стилтьеса

Пусть в промежутке заданы две ограниченные функции и . Разложим точками

(1)

промежуток на части и положим . Выбрав в каждой из частей по точке, вычислим значение функции и умножим его на соответствующее промежутку приращение функции

.

Наконец, составим сумму всех таких произведений:

. (2)

Эта сумма носит название интегральной суммы Стилтьеса.

Конечный предел суммы Стилтьеса при стремлении к нулю называется интегралом Стилтьеса функции по функции и обозначается символом

. (3)

Иной раз, желая особенно отчетливо подчеркнуть, что интеграл рассматривается в смысле Стилтьеса, употребляют обозначение

Предел здесь понимается в том же смысле, что и в случае обыкновенного определенного интеграла. Точнее говоря, число называется интегралом Стилтьеса, если для любого числа существует такое число , что лишь только промежуток раздроблен на части так, что , тотчас же выполняется неравенство

,

как бы не выбирать точки в соответствующих промежутках.