Дипломная работа: Качественное исследование в целом двумерной квадратичной стационарной системы с двумя частными интегралами в виде кривых третьего и первого порядков

x³ +a₁ x² y+b₁ xy² +g₁ y³ +a₂ x² +b₂ xy+g₂ y² +b₃ x+g₃ y+d=0, (0.4)

mx+ny+p=0 (0.5)

в предположении, что коэффициенты кривых (0.4), (0.5) и системы (0.3) вещественные.

Работа состоит из двух глав.

В первой главе проводится построение квадратичной двумерной стационарной системы с частными интегралами в виде кривых третьего и первого порядков. При этом коэффициенты интегралов выражаются через коэффициенты системы, а коэффициенты системы связаны между собой тремя соотношениями.

Во второй главе проводится качественное исследование системы, включающее в себя нахождение и исследование состояний равновесия, исследование бесконечно-удаленной части плоскости при фиксированных значениях коэффициентов системы.

1 ПОСТРОЕНИЕ КВАДРАТИЧНЫХ ДВУМЕРНЫХ СТАЦИОНАРНЫХ СИСТЕМ

1.1 Построение квадратичной двумерной стационарной системы с частным интегралом в виде кривой третьего порядка

Рассмотрим систему дифференциальных уравнений

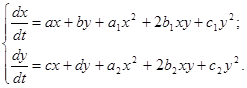(1.1)

Согласно [10, с. 1752-1760], если система, правые части которой есть полиномы n-ой степени, имеет частный интеграл вида:

, (1.2)

где F_k (x,y) – однородные полиномы от x и y степени k, то выполняется равенство:

. (1.3)

Пусть частный интеграл (1.2) имеет вид:

F(x,y)ºx³ +a₁ x² y+b₁ xy² +g₁ y³ +a₂ x² +b₂ xy+g₂ y² +b₃ x+g₃ y+d=0 (1.4)

Для интеграла (1.4) системы (1.1) имеет место соотношение (1.3),где L(x,y) = fx+gy+k, f, g, k – постоянные:

(3x2+2a₁ xy+b₁ y² +2a₂ x+b₂ y+b₃ )(ax+by+a₁ x² +2b₁ xy+c₁ y² )+(a₁ x² +

2b₁ xy+3g₁ y² +b₂ x+2g₂ y+g₃ )(cx+dy+a₂ x² +2b₂ xy+c₂ y² )=(x3+a₁ x² y+b₁ xy² + (1.5)

g₁ y³ +a₂ x² +b₂ xy+g₂ y² +b₃ x+g₃ y+d)(fx+gy+k).

Приравнивая в (1.5) коэффициенты при одинаковых степенях выражений

x^m yⁿ слева и справа, получим следующую связь между коэффициентами кривой (1.4) и системы (1.1):

3a₁₊ a₁ a₂ -f=0, (1.6₁ )

(2a₁ +2b₂ -f)a₁ +2a₂ b₁ -g+6b₁ =0, (1.6₂ )

2a₁ c₁ +(2b₁ +2c₂ -g)b₁ +(6b₂ -f)g₁ =0, (1.6₃ )

(4b₁ +c₂ -g)a₁ +(a₁ +4b₂ -f)b₁ +3a₂ g₁ +3c₁ =0, (1.6₄ )

c₁ b₁ +(3c₂ -g)g₁ =0; (1.6₅ )

ca₁ +(2a₁ -f)a₂ +a₂ b₂ -k+3a=0, (1.7₁ )

(2a+d-k)a₁ +2cb1+(4b₁ -g)a2+(a₁ +2b₂ -f)b2+2a₂ g₂ +3b=0, (1.7₂ )

2ba₁ +(a+2d-k)b₁ +3cg₁ +2c₁ a₂ +(2b₁ +c₂ -g)b₂ +(4b₂ -f)g₂ =0, (1.7₃ )