Дипломная работа: Качественное исследование в целом двумерной квадратичной стационарной системы с двумя частными интегралами в виде кривых третьего и первого порядков

,

Характеристическими числами для точки системы (2.1) будут

,

Корни - действительные и одного знака.Следовательно точка - устойчивый узел, если a>0 и неустойчивый узел, если a<0 .

2.2 Исследование бесконечно-удаленной части плоскости

Очень важным для исследования вопроса о наличии замкнутых траекторий являются сведения о поведении траекторий при удалении в бесконечность, то есть исследование бесконечно-удаленных частей плоскости.

Для этого воспользуемся преобразованием Пуанкаре [7]:

, (2.8)

которое позволяет изучить особые точки лежащие на экваторе сферы Пуанкаре вне концов оси OY.

Имеем

Значит преобразование (2.8) переводит систему (1.1) в систему:

(2.9)

Введем новое время . Система (2.9) примет вид:

(2.10)

Изучим бесконечно-удаленные точки на оси u, т.е. при z=0.

Получаем

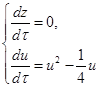(2.11)

Приравнивая второе уравнение системы (2.11) к нулю, получаем

Таким образом, состоянием равновесия являются две точки N₁ (0,0) N₂ (0,).

Исследуем характер точек N₁ , N₂ .

1. Исследуем точку N₁ (0,0).

Составим характеристическое уравнение системы (2.10) в точке N₁ :

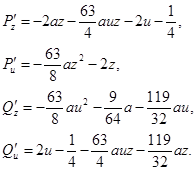(2.12)

Согласно выражениям (2.12), получаем характеристическое уравнение:

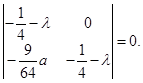
Получим, что