(a₁ -a)m= 0,

(3b₁ -b)n=0.

Пусть m¹0, тогда a₁ -a=0 и

a=a₁ , (1.24)

а при n¹0, получаем, что 3b₁ -b=0 и

b=3b_1. (1.25)

Учитывая (1.24) и (1.25) из условия (1.21₂ ) находим выражение коэффициента m:

m=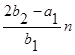, (1.26)

а соотношение (1.23₁ ) даст значение коэффициента p:

p=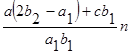. (1.27)

Из равенства (1.23₂ ), с учетом полученных выражений (1.26) и (1.27), находим условие на коэффициенты системы (1.1):

[3(a₁ b₁ -2b₁ b₂ ) a+(2a₁ b₂ -a₁ ² ) b-3b₁ ² c+a₁ b₁ d] n=0. (1.28)

Итак, установлена следующая теорема:

Теорема 1.2 Система (1.1) имеет частный интеграл (1.18), коэффициенты которого выражаются формулами (1.26),(1.27), при условии, что коэффициенты системы связаны соотношением (1.28) и c₁ =a₂ = 0, c₂ = 3b₁ .

1.3 Необходимые и достаточные условия существования у системы (1.1) двух частных интегралов (1.4), (1.18)

В разделах 1, 2 мы получили, что система (1.1) будет иметь два частных интеграла в виде кривых третьего и первого порядков при условии, что коэффициенты системы связаны соотношениями:

(2ab₁ -ba₁ )[3(32a₁ b₁ b₂ -15a₁ ² b₁ -16b₁ b₂ ² ) a+(8a₁ b₂ ² -18a₁ ² b₂ +9a₁ ³ ) b+

24(a₁ b₁ ² -b₁ ² b₂ ) c+(16a₁ b₁ b₂ -15a₁ ² b₁ ) d]=0,

(2ab₁ -ba₁ )[12(7a₁ b₁ b₂ -3a₁ ² b₁ -4b₁ b₂ ² ) a² +6(3a₁ b₁ ² -4b₁ ² b₂ ) ac+(3a₁ ² b₁ -

-4a₁ b₁ b₂ ) bc+2(4a₁ ² b₂ -3a₁ ³ )bd –8a₁ b₁ ² cd+4a₁ ² b₁ d² ]=0,

[3(a₁ b₁ -2b₁ b₂ ) a+(2a₁ b₂ -a₁ ² ) b-3b₁ ² c+a₁ b₁ d] n=0.

Причем b₁ ¹0, a₁ ¹0, 2b₁ a-ba₁ ¹0.

Рассмотрим частный случай, т.е. будем предполагать, что коэффициенты

a₁ =, b₁ =1, b₂ =0.

Следовательно, наши соотношения запишутся в виде:

a-b-3c+d=0, (1.30)

-a+b+6c-d=0, (1.31)

-a² +d² +ac+bc-bd-2cd=0. (1.32)

Выразим из условия (1.30) коэффициент c

c=a-b+d, (1.33)