Дипломная работа: Качественное исследование в целом двумерной квадратичной стационарной системы с двумя частными интегралами в виде кривых третьего и первого порядков

Корни - действительные и одного знака. Следовательно, точка N₁ (0,0) - устойчивый узел.

2. Исследуем точку N₂ (0,).

Учитывая выражение (2.12), составим характеристическое уравнение в точке N₂ :

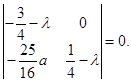
соответственно характеристическими числами будут являться

Корни - действительные и различных знаков. Следовательно, точка N₂ (0,)-седло.

Исследуем бесконечно-удаленную часть плоскости в конце оси OY с помощью преобразования [7]

Это преобразование систему (2.1) переводит в систему:

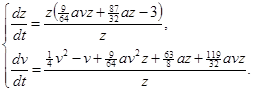(2.14)

Введем новое время , тогда система (2.14) примет следующий вид:

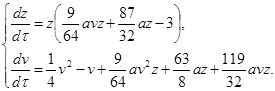(2.15)

При z=0, получаем:

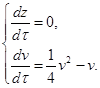(2.16)

Приравнивая второе уравнение системы (2.16) к нулю, получаем

Для исследования состояний равновесий на концах оси OY, необходимо исследовать только точку N₃ (0,0).

Составим характеристическое уравнение системы (2.16) в точке N₃ :

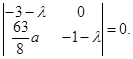
соответственно характеристическими числами будут являться

Корни - действительные и одного знака. Следовательно, точка N₃ (0,0) – устойчивый узел.

Теперь дадим распределение состояний равновесия системы (2.1) в виде таблицы 1.

Таблица 1.

a	О	А	В	С	∞
					N1	N2	N3
(-∞;0)	с	У+	с	У-	У+	с	У+
(0;+∞)	с	У-	с	У+	У+	с	У+

Примечание: через с, у⁺ , у^- обозначены соответственно седло, устойчивый узел, неустойчивый узел.

Положение кривых (1.4), (1.18) и расположение относительно их состояний равновесия при a>0 и a<0 дается соответственно рис. 1(а,б).