Дипломная работа: Качественное исследование в целом двумерной квадратичной стационарной системы с двумя частными интегралами в виде кривых второго порядка

Приравнивая коэффициенты при одинаковых степенях x^m yⁿ слева и справа, получим равенства:

(2a₁ -p) a₁ = 0 (1.5₁ )

(4b₁ -m) a₁ = 0 (1.5₂ )

2a₁ c₁ = 0 (1.5₃ )

(2a-n) a₁ + (a₁ -p) a₂ +a₂ = 0 (1.6₁ )

2a₁ b+ (2b₁ -m) a₂ +2b₂ +p= 0 (1.6₂ )

a₂ c₁ +c₂ -m= 0 (1.6₃ )

(a-n) a₂ -pa₃ n+c= 0 (1.7₁ )

a₂ b-a₃ m+d-n= 0 (1.7₂ )

a₃ n= 0 (1.7₃ )

Пусть a₁ ¹ 0, тогда из равенств (1.5₁ ), (1.5₂ ), (1.5₃ ), (1.6₃ ) и (1.7₃ ) получаем, что

P=2a₁ , m=4b₁ , c₁ =0, c₂ =4b₁ , n=0 (1.8)

Из соотношений (1.6₁ ), (1.6₂ ) и (1.7₁ ) найдем выражения коэффициентов кривой (1.3) через коэффициенты системы (1.1) в следующем виде:

a₁ , (1.9)

a₂ , (1.10)

a₃ . (1.11)

Равенство (1.7₂ ) с учетом полученных выражений (1.9) - (1.11), даст условие, связывающее коэффициенты a, b, c, d, a₁ , a₂ , b₁ , b₂ :

(1.12)

Итак, установлена следующая теорема:

Теорема 1.1 Система (1.1) имеет частный интеграл (1.3), коэффициенты которого выражаются формулами (1.9) - (1.11), при условии, что коэффициенты системы связаны соотношением (1.12) и c ₁ = 0, c ₂ = 4 b ₁ , a ₁ ¹ 0, 2 b ₁ a - a ₁ b ¹ 0.

1.2 Построение квадратичной двумерной стационарной системы с частным интегралом в виде окружности либо гиперболы

Пусть теперь система (1.1) наряду с интегралом (1.3) имеет интеграл в виде:

y² +sx² +bx+gy+d=0 (1.13)

Будем рассматривать теперь систему:

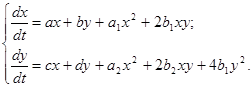(1.14)

Согласно формуле (1.4), где L

(x,y) = m₁ x+n₁ y+p₁ ,

m₁ , n₁ , p₁ - постоянные для системы (1.1), имеем:

(2a₁ -m₁ ) s² = 0 (1.15₁ )